
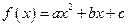
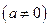 满足
满足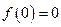 ,对于任意
,对于任意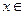 R都有
R都有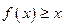 ,且
,且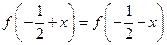 ,令
,令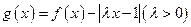 .
.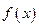 的表达式;
的表达式;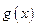 的单调区间;
的单调区间;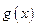 在区间
在区间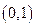 上的零点个数.
上的零点个数.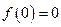 ,∴
,∴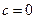 . …… 1分
. …… 1分 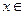 R都有
R都有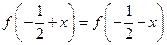 ,
,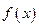 的对称轴为
的对称轴为 ,即
,即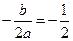 ,得
,得 . …… 2分
. …… 2分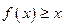 ,即
,即 对于任意
对于任意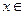 R都成立,
R都成立, ,且
,且
 .
. , ∴
, ∴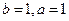 .
.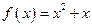 . …… 4分
. …… 4分
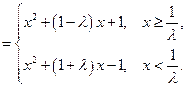 …… 5分
…… 5分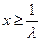 时,函数
时,函数 的对称轴为
的对称轴为 ,
, ,即
,即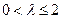 ,函数
,函数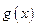 在
在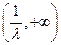 上单调递增; …… 6分
上单调递增; …… 6分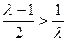 ,即
,即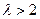 ,函数
,函数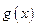 在
在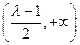 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.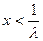 时,函数
时,函数 的对称轴为
的对称轴为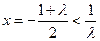 ,
,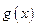 在
在 上单调递增,在
上单调递增,在 上单调递减. …… 8分
上单调递减. …… 8分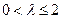 时,函数
时,函数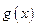 单调递增区间为
单调递增区间为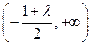 ,单调递减区间为
,单调递减区间为 ; …… 9分
; …… 9分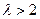 时,函数
时,函数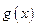 单调递增区间为
单调递增区间为 和
和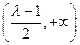 ,单调递减区间为
,单调递减区间为 和
和 . …… 10分
. …… 10分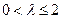 时,由(2)知函数
时,由(2)知函数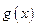 在区间
在区间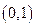 上单调递增,
上单调递增, ,
,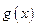 在区间
在区间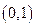 上只有一个零点. …… 11分
上只有一个零点. …… 11分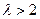 时,则
时,则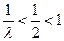 ,而
,而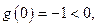
 ,
, ,
, ,由于
,由于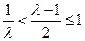 ,
,
 ,
,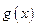 在区间
在区间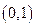 上只有一个零点; …… 12分
上只有一个零点; …… 12分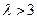 ,由于
,由于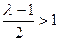 且
且
 ,此时,函数
,此时,函数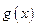 在区间
在区间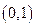
 时,函数
时,函数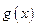 在区间
在区间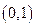 上只有一个零点;
上只有一个零点;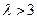 时,函数
时,函数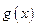 在区间
在区间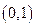 上有两个不同的零点. …… 14分
上有两个不同的零点. …… 14分

科目:高中数学 来源:不详 题型:解答题
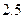 元的价格销售,可以售出
元的价格销售,可以售出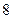 万本。据市场调查,若单价每提高
万本。据市场调查,若单价每提高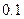 元,销售量就可能相应减少
元,销售量就可能相应减少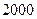 本。若要保证销售收入仍不低于
本。若要保证销售收入仍不低于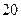 万元,应该怎样制定这种杂志的销售价格呢?
万元,应该怎样制定这种杂志的销售价格呢?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 。要求每天生产的乙种产品不能比甲种产品多10件以上,则合理安排生产可使每日获得的利润最大为( )
。要求每天生产的乙种产品不能比甲种产品多10件以上,则合理安排生产可使每日获得的利润最大为( )| A.500元 | B.700元 | C.400元 | D.650元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com