
【题目】对任意实数x和任意![]() ,恒有
,恒有![]() ,则实数a的取值范围为_____.
,则实数a的取值范围为_____.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 任作一条与两条坐标轴都不垂直的直线,与椭圆
任作一条与两条坐标轴都不垂直的直线,与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8,当直线
的周长为8,当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 与
与![]() 轴垂直.
轴垂直.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,总能使
,总能使![]() 平分
平分![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知底面ABCD是矩形,PA⊥平面ABCD,AP=2,AB=2,AD=4,且E、F分别是PB、PC的中点。
中,已知底面ABCD是矩形,PA⊥平面ABCD,AP=2,AB=2,AD=4,且E、F分别是PB、PC的中点。
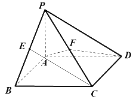
(1)求三棱锥![]() 的体积;
的体积;
(2)求直线EC与平面PCD所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海途安型号出租车价格规定:起步费![]() 元,可行
元,可行![]() 千米;
千米;![]() 千米以后按每千米按
千米以后按每千米按![]() 元计价,可再行
元计价,可再行![]() 千米;以后每千米都按
千米;以后每千米都按![]() 元计价。假如忽略因交通拥挤而等待的时间.
元计价。假如忽略因交通拥挤而等待的时间.
![]() 请建立车费
请建立车费![]() (元)和行车里程
(元)和行车里程![]() (千米)之间的函数关系式;
(千米)之间的函数关系式;
![]() 注意到上海出租车的计价系统是以元为单位计价的,如:小明乘坐途安型号出租车从华师大二附中本部到浦东实验学校走路线一(路线一总长
注意到上海出租车的计价系统是以元为单位计价的,如:小明乘坐途安型号出租车从华师大二附中本部到浦东实验学校走路线一(路线一总长![]() 千米)须付车费
千米)须付车费![]() 元,走路线二(路线二总长
元,走路线二(路线二总长![]() 千米)也须付车费
千米)也须付车费![]() 元.将上述函数解析式进行修正(符号
元.将上述函数解析式进行修正(符号![]() 表示不大于
表示不大于![]() 的最大整数,符号
的最大整数,符号![]() 表示不小于
表示不小于![]() 的最小整数);并求小明乘坐途安型号出租车从华师大二附中本部到闵行分校须付车费多少元?(注:两校区路线长
的最小整数);并求小明乘坐途安型号出租车从华师大二附中本部到闵行分校须付车费多少元?(注:两校区路线长![]() 千米)
千米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阀值与检验》国家标准.新标准规定,车辆驾驶人员血液中的酒精含量大于或等于![]() 毫克/百毫升,小于
毫克/百毫升,小于![]() 毫克/百毫升为饮酒驾车,血液中的酒精含量大于或等于
毫克/百毫升为饮酒驾车,血液中的酒精含量大于或等于![]() 毫克/百毫升为醉酒驾车.经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下图,该函数近似模型如下:
毫克/百毫升为醉酒驾车.经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下图,该函数近似模型如下: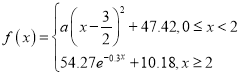 .
.
又已知刚好过1小时时测得酒精含量值为![]() 毫克/百毫升.根据上述条件,解答以下问题:
毫克/百毫升.根据上述条件,解答以下问题:
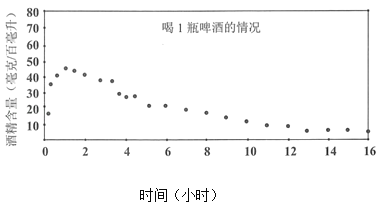
(1)试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整分钟计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
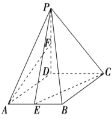
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,记该数列前
,记该数列前![]() 项
项![]() 中的最大项为
中的最大项为![]() ,即
,即![]() ,该数列后
,该数列后![]() 项
项![]() 中的最小项为
中的最小项为![]() ,记
,记![]() ,
,![]() ;
;
(1)对于数列:3,4,7,1,求出相应的![]() ,
,![]() ,
,![]() ;
;
(2)若![]() 是数列
是数列![]() 的前
的前![]() 项和,且对任意
项和,且对任意![]() ,有
,有![]() ,其中
,其中![]() 为实数,
为实数,![]() 且
且![]() ,
,![]() .
.
(ⅰ)设![]() ,证明:数列
,证明:数列![]() 是等比数列;
是等比数列;
(ⅱ)若数列![]() 对应的
对应的![]() 满足
满足![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 、
、![]() .
.
(1)求以![]() 为焦点,原点为顶点的抛物线方程;
为焦点,原点为顶点的抛物线方程;
(2)若椭圆![]() 上点
上点![]() 满足
满足![]() ,求
,求![]() 的纵坐标
的纵坐标![]() ;
;
(3)设![]() ,若椭圆
,若椭圆![]() 上存在两个不同点
上存在两个不同点![]() 、
、![]() 满足
满足![]() ,证明:直线
,证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com