
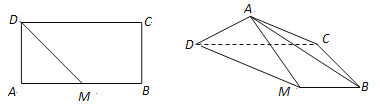
【题目】如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知从![]() 地到
地到![]() 地有两条道路可以到达,走道路①准点到达的概率为
地有两条道路可以到达,走道路①准点到达的概率为![]() ,不准点到达的概率为
,不准点到达的概率为![]() ;走道路②准点到达的概率为
;走道路②准点到达的概率为![]() ,不准点到达的概率为
,不准点到达的概率为![]() .若甲乙两车走道路①,丙车由于其他原因走道路②,且三辆车是否准点到达相互之间没有影响.
.若甲乙两车走道路①,丙车由于其他原因走道路②,且三辆车是否准点到达相互之间没有影响.
(1)若三辆车中恰有一辆车没有准点到达的概率为![]() ,求走道路②准点到达的概率
,求走道路②准点到达的概率![]() ;
;
(2)在(1)的条件下,求三辆车中准点到达车辆的辆数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率是
的离心率是![]() ,A、B分别为椭圆的左顶点、上顶点,原点O到AB所在直线的距离为
,A、B分别为椭圆的左顶点、上顶点,原点O到AB所在直线的距离为![]() .
.
(I)求椭圆C的方程;
(Ⅱ)已知直线![]() 与椭圆相交于不同的两点M,N(均不是长轴的端点),
与椭圆相交于不同的两点M,N(均不是长轴的端点),![]() ,垂足为H,且
,垂足为H,且![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率,;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出
(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出![]() 的所有可能值,并估计
的所有可能值,并估计![]() 大于零的概率.
大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,在高三年级中随机选取![]() 名学生进行跟踪问卷,其中每周线上学习数学时间不少于
名学生进行跟踪问卷,其中每周线上学习数学时间不少于![]() 小时的有
小时的有![]() 人,在这
人,在这![]() 人中分数不足
人中分数不足![]() 分的有
分的有![]() 人;在每周线上学习数学时间不足于
人;在每周线上学习数学时间不足于![]() 小时的人中,在检测考试中数学平均成绩不足
小时的人中,在检测考试中数学平均成绩不足![]() 分的占
分的占![]() .
.
(1)请完成![]() 列联表;并判断是否有
列联表;并判断是否有![]() 的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
分数不少于 | 分数不足 | 合计 | |
线上学习时间不少于 | |||
线上学习时间不足 | |||
合计 |
(2)在上述样本中从分数不足于![]() 分的学生中,按照分层抽样的方法,抽到线上学习时间不少于
分的学生中,按照分层抽样的方法,抽到线上学习时间不少于![]() 小时和线上学习时间不足
小时和线上学习时间不足![]() 小时的学生共
小时的学生共![]() 名,若在这
名,若在这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求这
人,求这![]() 人每周线上学习时间都不足
人每周线上学习时间都不足![]() 小时的概率.(临界值表仅供参考)
小时的概率.(临界值表仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式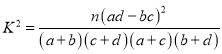 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为抛物线
为抛物线![]() 外一点,过点
外一点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.

(Ⅰ)若点![]() 为
为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 为圆
为圆![]() 上的点,记两切线
上的点,记两切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拿破仑为人好学,是法兰西科学院院士,他对数学方面很感兴趣,在行军打仗的空闲时间,经常研究平面几何。他提出了著名的拿破仑定理:以三角形各边为边分别向外(内)侧作等边三角形,则它们的中心构成一个等边三角形。如图所示,以等边![]() 的三条边为边,向外作
的三条边为边,向外作![]() 个正三角形,取它们的中心
个正三角形,取它们的中心![]() ,顺次连接,得到
,顺次连接,得到![]() ,图中阴影部分为
,图中阴影部分为![]() 与
与![]() 的公共部分。若往
的公共部分。若往![]() 中投掷一点,则该点落在阴影部分内的概率为( )
中投掷一点,则该点落在阴影部分内的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.

(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com