(1)过一点向平面引垂线,________叫做这个点在这个平面内的射影;当这一点在平面内时,该点在平面上的射影就是它______;这一点与_______的线段叫做这点到这个平面的_______.如图所示,直线
PQ⊥
α,
Q∈
α,则点
Q是______在平面
α内的_____,线段_______是点_______到平面
α的______.?

(2)一条直线和一个平面相交,但不______时,这条直线就叫做这个平面的_______,斜线与平面的交点叫做_____.从平面外一点向平面引斜线,这点与________间的线段叫做这点到这个平面的_______.如图所示,直线PR∩α=R,PR不______于α,直线PR是α的一条_____,点R为_______,线段_____是点P到α的______.?
(3)平面外一点到这个平面的垂线段______条,而这点到这个平面的______有无数条.?
(4)从斜线上斜足以外的一点向平面引垂线,过垂足的直线叫做斜线在这个平面内的_______,________与________间的线段叫做这点到平面的斜线段在这个平面内的________.如图所示,直线_____是直线PR在平面α上的______,线段______是点P到平面α的斜线段PR在平面α上的射影.?
(5)斜线上任意一点在平面上的射影一定在斜线的_____上.事实上,设a是平面α的斜线,B为斜足,在a上任取一点A,作AA1⊥α,A1是垂足,则A1、B确定的直线a′是a在平面α内的______,如图所示,设P是a上任意一点,在a和AA1确定的平面内,作PP1∥AA1,PP1必与a′相交于一点P1.∵AA1α__________ ,PP1______________AA1,∴PP1__________α.P1为P在平面α上的射影,所以点P在平面α上的射影一定在直线a在平面α上的射影a′上.


 =
=
 +
+
 ,则△ABP与△ABC的面积之比等于( )
,则△ABP与△ABC的面积之比等于( )




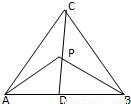 解:连接CP并延长交AB于D,
解:连接CP并延长交AB于D,

 阅读快车系列答案
阅读快车系列答案

 =
=
 +
+
 ,则△ABP与△ABC的面积之比等于( )
,则△ABP与△ABC的面积之比等于( )



