
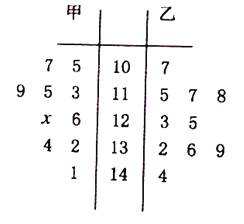
【题目】为了减少雾霾,还城市一片蓝天,某市政府于12月4日到12月31日在主城区实行车辆限号出行政策,鼓励民众不开车低碳出行,某甲乙两个单位各有200名员工,为了了解员工低碳出行的情况,统计了12月5日到12月14日共10天的低碳出行的人数,画出茎叶图如下:
(1)若甲单位数据的平均数是122,求![]() ;
;
(2)现从如图的数据中任取4天的数据(甲、乙两单位中各取2天),记其中甲、乙两单位员工低碳出行人数不低于130人的天数为![]() ,
, ![]() ,令
,令![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
科目:高中数学 来源: 题型:
【题目】
近年来,随着双十一、双十二等网络活动的风靡,各大网商都想出了一系列的降价方案,以此来提高自己的产品利润. 已知在2016年双十一某网商的活动中,某店家采取了两种优惠方案以供选择:
方案一:购物满400元以上的,超出400元的部分只需支出超出部分的x%;
方案二:购物满400元以上的,可以参加电子抽奖活动,即从1,2,3,4,5,6这6张卡牌中任取2张,将得到的数字相加,所得结果与享受优惠如下:
数字和 | [3,4] | [5,7] | [8,9] | [10,11] |
实际付款 | 原价 | 9折 | 8折 | 5折 |
(Ⅰ)若某顾客消费了800元,且选择方案二,求该顾客只需支付640元的概率;
(Ⅱ)若某顾客购物金额为500元,她选择了方案二后,得到的数字之和为6,此时她发现使用方案一、二最后支付的金额相同,求x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-aln x(a>0)的最小值是1.
(1)求a;
(2)若关于x的方程f2(x)ex-6mf(x)+9me-x=0在区间[1,+∞)有唯一的实根,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x+ax-![]() +b.
+b.
(1)若函数g(x)=f(x)+![]() 为减函数,求实数a的取值范围;
为减函数,求实数a的取值范围;
(2)若f(x)≤0恒成立,证明:a≤1-b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试,成绩如茎叶图所示.
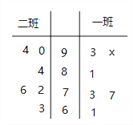
(1)若一班、二班6名学生的平均分相同,求![]() 值;
值;
(2)若将竞赛成绩在![]() 、
、![]() 、
、![]() 内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)经过点(
(a>b>0)经过点(![]() ,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得![]() 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax+2lnx,a∈R.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线垂直于直线y=x,求函数f(x)的单调区间;
(Ⅱ)若x>1时,f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856287)
已知点A(0,1)与B(![]() ,
, ![]() )都在椭圆C:
)都在椭圆C: ![]() (a>b>0)上,直线AB交x轴于点M.
(a>b>0)上,直线AB交x轴于点M.
(Ⅰ)求椭圆C的方程,并求点M的坐标;
(Ⅱ)设O为原点,点D与点B关于x轴对称,直线AD交x轴于点N.问:y轴上是否存在点E,使得∠OEM=∠ONE?若存在,求点E的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com