
【题目】某创新团队拟开发一种新产品,根据市场调查估计能获得10万元到1000万元的收益,先准备制定一个奖励方案:奖金![]() (单位:万元)随收益
(单位:万元)随收益![]() (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过收益的20%.
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过收益的20%.
(1)若建立函数![]() 模型制定奖励方案,试用数学语言表示该团队对奖励函数
模型制定奖励方案,试用数学语言表示该团队对奖励函数![]() 模型的基本要求,并分析
模型的基本要求,并分析![]() 是否符合团队要求的奖励函数模型,并说明原因;
是否符合团队要求的奖励函数模型,并说明原因;
(2)若该团队采用模型函数![]() 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某次电影展,有14部参赛影片,组委会分两天在某一影院播映这14部电影,每天7部,其中有2部4D电影要求不在同一天放映,下列不能作为排片方案数的计算式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆C上,且
在椭圆C上,且![]() ⊥
⊥![]()
![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() .
.
(1)求椭圆C的标准方程;
(2)已知直线l与椭圆C交于A,B两点,![]() ,若直线l始终与圆
,若直线l始终与圆![]() 相切,求半径r的值.
相切,求半径r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线![]() 垂直于
垂直于![]() 轴,与椭圆
轴,与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,
上,![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,与曲线
,与曲线![]() 相切于点
相切于点![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 上的点
上的点![]() 到焦点
到焦点![]() 的距离为2.
的距离为2.
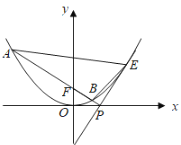
(1)求抛物线的方程;
(2)如图,点![]() 是抛物线上异于原点的点,抛物线在点
是抛物线上异于原点的点,抛物线在点![]() 处的切线与
处的切线与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,求
两点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com