
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
【答案】C
【解析】解:A.f(x)的定义域为R,而g(x)的定义域为(0,+∞),所以定义域不同,所以A不是同一函数.
B.f(x)的定义域为R,而g(x)= ![]() =x+1,(x≠1),则g(x)的定义域为(﹣∞,1)∪(1,+∞),所以定义域不同,所以B不是同一函数.
=x+1,(x≠1),则g(x)的定义域为(﹣∞,1)∪(1,+∞),所以定义域不同,所以B不是同一函数.
C.因为g(x)=|x|,所以两个函数的定义域和对应法则一致,所以C表示同一函数.
D.f(x))=log22x=x,则f(x)的定义域为R,而g(x)的定义域为(0,+∞),所以定义域不同,所以D不是同一函数.
故选:C.
【考点精析】关于本题考查的判断两个函数是否为同一函数,需要了解只有定义域和对应法则二者完全相同的函数才是同一函数才能得出正确答案.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )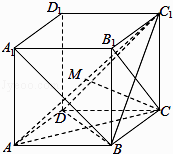
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4sinx(cosx﹣sinx)+3 (Ⅰ)当x∈(0,π)时,求f(x)的单调递减区间;
(Ⅱ)若f(x)在[0,θ]上的值域为[0,2 ![]() +1],求cos2θ的值.
+1],求cos2θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=| ![]() ﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
A.(﹣∞,0]
B.(﹣∞,1]
C.(﹣∞,2]
D.(﹣∞,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一辆汽车在某段路程中的行驶速率与时间的关系如图所示. 
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车在行驶该段路程前里程表的读数是8018km,试求汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并作出相应的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=log2(2x+1)的图象,只需将y=1+log2x的图象( )
A.向左移动 ![]() 个单位
个单位
B.向右移动 ![]() 个单位
个单位
C.向左移动1个单位
D.向右移动1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,a2=6,且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列.
(1)求{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 求满足不等式Sn>
}的前n项和为Sn , 求满足不等式Sn> ![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4y﹣4=0,是否存在斜率为1的直线l,使l被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程l,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com