
| A. | (-2,-4) | B. | $(-\frac{1}{2},-1)$ | C. | (-2,-4)或$(-\frac{1}{2},-1)$ | D. | 不确定 |
分析 由已知可得a2=a+2≠0,解得a=-1或a=2,把a=-1代入原方程,配方求得圆心坐标和半径,把a=2代入原方程,由D2+E2-4F<0说明方程不表示圆,则答案可求.
解答 解:∵方程a2x2+(a+2)y2+4x+8y+5a=0表示圆,
∴a2=a+2≠0,解得a=-1或a=2.
当a=-1时,方程化为x2+y2+4x+8y-5=0,
配方得(x+2)2+(y+4)2=25,所得圆的圆心坐标为(-2,-4),半径为5;
当a=2时,方程化为x2+y2+x+2y+2.5=0,
此时D2+E2-4F<0,方程不表示圆,
故选:A.
点评 本题考查圆的一般方程,考查圆的一般方程化标准方程,是中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
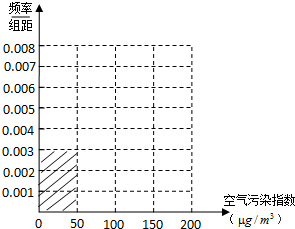
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | ||
| C. | 第一象限或第三象限 | D. | 第三象限或第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
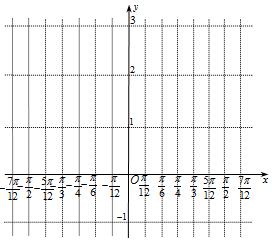 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4π}{3}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com