
【题目】某厂生产![]() 和
和![]() 两种产品,按计划每天生产
两种产品,按计划每天生产![]() 各不得少于10吨,已知生产
各不得少于10吨,已知生产![]() 产品
产品![]() 吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产
吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产![]() 产品1吨需要用煤4吨,电5度,劳动力10个,如果
产品1吨需要用煤4吨,电5度,劳动力10个,如果![]() 产品每吨价值7万元,
产品每吨价值7万元, ![]() 产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产
产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产![]() 两种产品各多少才是合理的?
两种产品各多少才是合理的?
【答案】![]() 产品20吨和
产品20吨和![]() 产品
产品![]() 吨是合理的.
吨是合理的.
【解析】试题分析:设每天生产![]() 产品
产品![]() 吨和
吨和![]() 产品
产品![]() 吨,根据用煤量、用电量、劳动力的限制列出关于,
吨,根据用煤量、用电量、劳动力的限制列出关于, ![]() 的约束条件,画出可行域,平移目标函数
的约束条件,画出可行域,平移目标函数![]() ,即可找到最优解,代入目标函数即可得结果.
,即可找到最优解,代入目标函数即可得结果.
试题解析:设每天生产![]() 产品
产品![]() 吨和
吨和![]() 产品
产品![]() 吨,则创造的价值为
吨,则创造的价值为![]() (万元),由已知列出的约束条件为
(万元),由已知列出的约束条件为
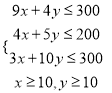 ,问题就成为在此二元一次不等式组限制的范围(区域)内寻找
,问题就成为在此二元一次不等式组限制的范围(区域)内寻找![]() ,使目标函数
,使目标函数![]() 取最大值的问题,画出可行域如图.
取最大值的问题,画出可行域如图.
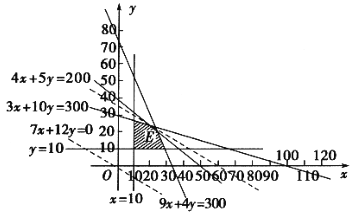
∵![]() ,∴当直线
,∴当直线![]() 经过直线
经过直线![]() 与
与![]() 的交点
的交点![]() 时,
时, ![]() 最大,解方程组
最大,解方程组![]() 得
得![]() ,∴
,∴![]() 点坐标为
点坐标为![]() ,∴当
,∴当![]() 时,
时, ![]() 取最大值.
取最大值.
答:每天生产![]() 产品20吨和
产品20吨和![]() 产品
产品![]() 吨是合理的.
吨是合理的.
【方法点晴】本题主要考查线性规划的应用、利用可行域求目标函数的最值,属中档题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,
, ![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,且
,且![]() ,求函数
,求函数![]() 在
在![]() 上的最小值及相应的
上的最小值及相应的![]() 值;
值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在研究某种药物对“H1N11”病毒的治疗效果时,进行动物试验,得到以下数据,对146只动物服用药物,其中101只动物存活,45只动物死亡;对照组144只动物进行常规治疗,其中124只动物存活,20只动物死亡.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)试问该种药物对治疗“H1N1”病毒是否有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com