
【题目】如图,三棱锥P﹣ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA. 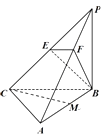
(1)求证:BE⊥平面PAC;
(2)求证:CM∥平面BEF;
(3)求平面ABC与平面BEF所成的二面角的平面角(锐角)的余弦值.
【答案】
(1)证明:∵BP=BC,EP=EC,∴BE⊥PC.
∵PB⊥底面ABC,∴PB⊥AC,
又AC⊥BC,PB∩BC=B,∴AC⊥平面PBC,
∴AC⊥BE.
又PC∩AC=C,∴BE⊥平面PAC.
(2)证明:取AF得中点Q,连接CQ,MQ.
∵2PF=FA,∴点F为PQ的中点,
由三角形的中位线定理可得EF∥CQ,BF∥MQ,
又CQ∩MQ=Q,∴平面BEF∥平面CMQ,
∴CM∥平面BEF.
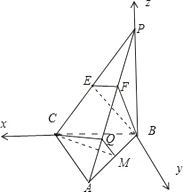
(3)证明:建立如图所示的空间直角坐标系,
则B(0,0,0),P(0,0,2),C(2,0,0),A(2,2,0),E(1,0,1),F ![]() .
.
![]() ,
, ![]() .
.
设平面BEF的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 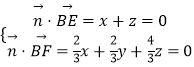 ,令x=1,则z=﹣1,y=1.
,令x=1,则z=﹣1,y=1.
∴ ![]() =(1,1,﹣1).取平面ABC的法向量
=(1,1,﹣1).取平面ABC的法向量 ![]() .
.
则 ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴平面ABC与平面BEF所成的二面角的平面角(锐角)的余弦值为 ![]() .
.
【解析】(1)利用等腰三角形的性质可得BE⊥PC.再利用线面垂直的判定和性质即可证明BE⊥平面PAC;(2)取AF得中点Q,连接CQ,MQ.利用已知及三角形的中位线定理可得EF∥CQ,BF∥MQ,即可得到面面平行:平面BEF∥平面CMQ,进而得到线面平行;(3)通过建立空间直角坐标系,利用两个平面的法向量即可得出.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , a1=10,an+1=9Sn+10.
(1)求证:{lgan}是等差数列;
(2)设 ![]() 对所有的n∈N*都成立的最大正整数m的值.
对所有的n∈N*都成立的最大正整数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①如果向量 ![]() ,
, ![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么 ![]() ,
, ![]() 的关系是不共线;
的关系是不共线;
②O,A,B,C为空间四点,且向量 ![]() ,
, ![]() ,
, ![]() 不构成空间的一个基底,则点O,A,B,C一定共面;
不构成空间的一个基底,则点O,A,B,C一定共面;
③已知向量 ![]() ,
, ![]() ,
, ![]() 是空间的一个基底,则向量
是空间的一个基底,则向量 ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() 也是空间的一个基底;
也是空间的一个基底;
④△ABC中,A>B的充要条件是sinA>sinB.
其中正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() ,点
,点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,与曲线
,与曲线![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com