
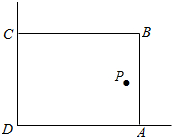
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.分析 (1)AD长为x,则CD长为16-x,由题意可得a≤x≤12,运用矩形的面积公式,即可得到所求解析式和定义域;
(2)讨论a的范围,当0<a≤4时,当4<a≤8时,当8<a<12时,结合二次函数的对称轴和单调性,即可得到最值,进而得到g(a)的解析式.
解答 解:(1)AD长为x,则CD长为16-x,
又因为要将P点围在矩形ABCD内,
∴a≤x≤12,
则矩形ABCD的面积为y=f(x)=x(16-x),定义域为[a,12];
(2)当0<a≤4时,当且仅当x=8时,f(x)取得最大值64,
x=a时,取得最小值,且为a(16-a),可得g(a)=64-16a+a2;
当4<a≤8时,f(x)的最大值为64,最小值为12×(16-12)=48,
g(a)=64-48=16;
当8<a<12时,[a,12]为递减区间,可得:
f(x)的最大值为a(16-a),最小值为48,
即有g(a)=16a-a2-48.
则有g(a)=$\left\{\begin{array}{l}{64-16a+{a}^{2},0<a≤4}\\{16,4<a≤8}\\{16a-{a}^{2}-48,8<a<12}\end{array}\right.$.
点评 本题考查二次函数的解析式和最值的求法,注意运用分类讨论的思想方法,属于中档题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | (-$\frac{π}{8}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
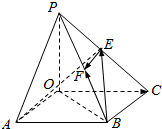 如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 每池产量 | 1万只 | 1.2万只 | 1.4万只 | 1.6万只 | 1.8万只 | 2万只 |
| 年 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 鱼池个数 | 30个 | 26个 | 22个 | 18个 | 14个 | 10个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com