
求证:平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形.
 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
(06年山东卷理)(12分)
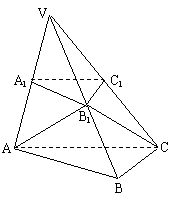
如图,已知平面![]() 平行于三棱锥
平行于三棱锥![]() 的底面ABC,等边△
的底面ABC,等边△![]() 所在的平面与底面ABC垂直,且∠ACB=90°,设
所在的平面与底面ABC垂直,且∠ACB=90°,设![]()
(1)求证直线![]() 是异面直线
是异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角![]() 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com