
【题目】已知函数![]() ,
, ![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上有1个零点,求实数
上有1个零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() ,使得
,使得![]() 在
在![]() 上恒成立?若存在,求出k的最大值;若不存在,说明理由.
上恒成立?若存在,求出k的最大值;若不存在,说明理由.
【答案】(1)见解析;(2) ![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)当![]() 时,得到
时,得到![]() ,求得
,求得![]() ,利用
,利用![]() 和
和![]() ,即可求解函数的单调区间;
,即可求解函数的单调区间;
(2)由![]() ,分
,分![]() 和
和![]() 两种情况分类讨论,得到函数的单调性与极值,结合函数的图象,即可求解实数
两种情况分类讨论,得到函数的单调性与极值,结合函数的图象,即可求解实数![]() 的取值范围;
的取值范围;
(3)假设存在正整数![]() ,使得
,使得![]() 在
在![]() 上恒成立,分类参数得出
上恒成立,分类参数得出![]() 对
对![]() 恒成立,设函数
恒成立,设函数![]() ,求得
,求得![]() ,求得函数
,求得函数![]() 单调性与极值,即可求解实数
单调性与极值,即可求解实数![]() 的最大值.
的最大值.
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() .
.
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)![]() ,
,
当![]() 时,由
时,由![]() ,知
,知![]() ,
,
所以, ![]() 在
在![]() 上是单调增函数,且图象不间断,
上是单调增函数,且图象不间断,
又![]() ,∴当
,∴当![]() 时,
时, ![]() ,
,
∴函数![]() 在区间
在区间![]() 上没有零点,不合题意.
上没有零点,不合题意.
当![]() 时,由
时,由![]() ,解得
,解得![]() ,
,
若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是单调减函数,
上是单调减函数,
若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是单调增函数,
上是单调增函数,
∴当![]() 时,
时, ![]() ,
,
又∵![]() ,
, ![]() 在
在![]() 上的图象不间断,
上的图象不间断,
∴函数![]() 在区间
在区间![]() 上有1个零点,符合题意.
上有1个零点,符合题意.
综上所述, ![]() 的取值范围为
的取值范围为![]() .
.
(3)假设存在正整数![]() ,使得
,使得![]() 在
在![]() 上恒成立,
上恒成立,
则由![]() 知
知![]() ,从而
,从而![]() 对
对![]() 恒成立(*)
恒成立(*)
记![]() ,得
,得![]() ,
,
设![]() ,
, ![]() ,
,
∴![]() 在
在![]() 是单调增函数,
是单调增函数,
又![]() 在
在![]() 上图象是不间断的,
上图象是不间断的,
∴存在唯一的实数![]() ,使得
,使得![]() ,
,
∴当![]() 时,
时, ![]() 在
在![]() 上递减,
上递减,
当![]() 时,
时, ![]() 在
在![]() 上递增,
上递增,
∴当![]() 时,
时, ![]() 有极小值,即为最小值,
有极小值,即为最小值, ![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴ ![]() ,
,
由(*)知, ![]() ,又
,又![]() ,
, ![]() ,∴
,∴ ![]() 的最大值为3,
的最大值为3,
即存在最大的正整数![]() ,使得
,使得![]() 在
在![]() 上恒成立.
上恒成立.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.
规定:每辆自行车的日租金不超过20元,每辆自行车的日租金x元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用y表示出租所有自行车的日净收入(即一日中出租所有自行车的总收入减去管理费后的所得).
(1)求函数y=f(x)的解析式及定义域;
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2 ![]() km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
km.现欲在此地块内建一形状为直角梯形DECF的科技园区. 
(1)求此曲边三角形地块的面积;
(2)求科技园区面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》里面提出“新建住宅要推广街区制,原则上不再建设封闭住宅小区,已建成的封闭小区和单位大院要逐步打开”,这个消息在网上一石激起千层浪,各种说法不一而足.某网站为了解居民对“开放小区”认同与否,从![]() 岁的人群中随机抽取了
岁的人群中随机抽取了![]() 人进行问卷调查,并且做出了各个年龄段的频率分布直方图(部分)如图所示,同时对
人进行问卷调查,并且做出了各个年龄段的频率分布直方图(部分)如图所示,同时对![]() 人对这“开放小区”认同情况进行统计得到下表:
人对这“开放小区”认同情况进行统计得到下表:
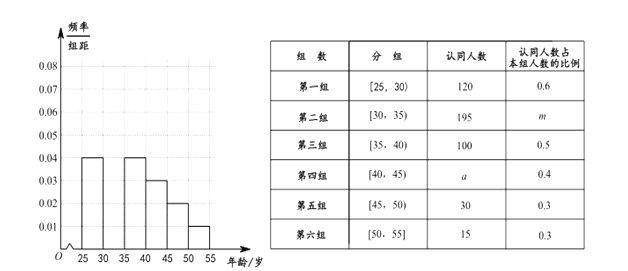
(Ⅰ)完成所给的频率分布直方图,并求![]() 的值;
的值;
(Ⅱ)如果从![]() 两个年龄段中的“认同”人群中,按分层抽样的方法抽取6人参与座谈会,然后从这6人中随机抽取2人作进一步调查,求这2人的年龄都在
两个年龄段中的“认同”人群中,按分层抽样的方法抽取6人参与座谈会,然后从这6人中随机抽取2人作进一步调查,求这2人的年龄都在![]() 内的概率 .
内的概率 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com