
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上为减函数,求实数
上为减函数,求实数![]() 的最小值;
的最小值;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)最小值为![]() .(2)
.(2)![]()
【解析】
(1)根据题意,确定函数定义域,然后求导,若函数![]() 在
在![]() 上为减函数,则
上为减函数,则![]() 在
在![]() 上恒成立,转化不等式为
上恒成立,转化不等式为![]() ,令
,令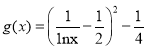 ,求解
,求解![]() 的最小值,则
的最小值,则![]() ,即可求解参数最值.
,即可求解参数最值.
(2)问题等价于当![]() 时,有
时,有![]() ,通过讨论
,通过讨论![]() 的范围,得到函数的单调区间,从而求出
的范围,得到函数的单调区间,从而求出![]() 的具体范围即可.
的具体范围即可.
(1)由已知得![]() 的定义域
的定义域![]() ,
,
∵![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,
,
令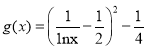 ,故当
,故当![]() ,即
,即![]() 时,
时,
![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,即
,即![]() ∴
∴![]() 的最小值为
的最小值为![]() .
.
(2)命题“若存在![]() ,使
,使![]() 成立”,
成立”,
等价于“当![]() 时,有
时,有![]() ”,
”,
由(1)知,当![]() 时,
时,![]() ,
,![]() ,
,
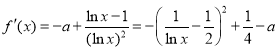 ,
,
![]() ,
,
问题等价于:“当![]() 时,有
时,有![]() ”,
”,
①当![]() ,即
,即![]() 时,由(1),
时,由(1),![]() 在
在![]() 上为减函数,
上为减函数,
则![]() .
.
②当![]() ,即
,即![]() 时,
时,![]() ,
,
∵![]() ,由复合函数的单调性知
,由复合函数的单调性知![]() 在
在![]() 上为增函数,
上为增函数,
∴存在唯![]() ,使
,使![]() 且满足:
且满足:
![]() ,
,
要使![]() ,
,
与![]() 矛盾,∴
矛盾,∴![]() 不合题意.
不合题意.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .当销售数据
.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从
称为一个“好数据”.现从![]() 个销售数据中任取
个销售数据中任取![]() 个子,求“好数据”个数
个子,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为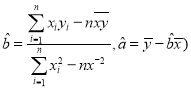 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
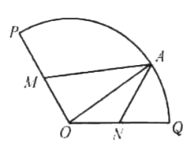
【题目】某校有一块圆心![]() ,半径为200米,圆心角为
,半径为200米,圆心角为![]() 的扇形绿地
的扇形绿地![]() ,半径
,半径![]() 的中点分别为
的中点分别为![]() ,
,![]() 为弧
为弧![]() 上的一点,设
上的一点,设![]() ,如图所示,拟准备两套方案对该绿地再利用.
,如图所示,拟准备两套方案对该绿地再利用.
(1)方案一:将四边形绿地![]() 建成观赏鱼池,其面积记为
建成观赏鱼池,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
(2)方案二:将弧![]() 和线段
和线段![]() 围成区域建成活动场地,其面积记为
围成区域建成活动场地,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式;并求
的函数关系式;并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下有关命题的说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”成立的必要不充分条件
”成立的必要不充分条件
C.对于命题![]() ,使得
,使得![]() ,则
,则![]() ,均有
,均有![]()
D.若![]() 为真命题,则
为真命题,则![]() 与
与![]() 至少有一个为真命题
至少有一个为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城.其中著名的景点有黄鹤楼、户部巷、东湖风景区等等.
(1)为了解“五·一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在22岁到52岁的游客中随机抽取了1000人,制成了如图的频率分布直方图:
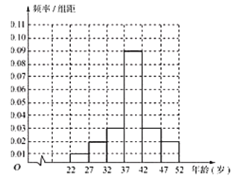
现从年龄在![]() 内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在
内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() ;
;
(2)为了给游客提供更舒适的旅游体验,该旅游景点游船中心计划在2020年劳动节当日投入至少1艘至多3艘![]() 型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量
型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量![]() (单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
(单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
劳动节当日客流量 |
|
|
|
频数(年) | 2 | 4 | 4 |
以这10年的数据资料记录的3个区间客流量的频率作为每年客流量在该区间段发生的概率,且每年劳动节当日客流量相互独立.
该游船中心希望投入的![]() 型游船尽可能被充分利用,但每年劳动节当日
型游船尽可能被充分利用,但每年劳动节当日![]() 型游船最多使用量(单位:艘)要受当日客流量
型游船最多使用量(单位:艘)要受当日客流量![]() (单位:万人)的影响,其关联关系如下表:
(单位:万人)的影响,其关联关系如下表:
劳动节当日客流量 |
|
| |
| 1 | 2 | 3 |
若某艘![]() 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘
型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘![]() 型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记
型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记![]() (单位:万元)表示该游船中心在劳动节当日获得的总利润,
(单位:万元)表示该游船中心在劳动节当日获得的总利润,![]() 的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘
的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘![]() 型游船才能使其当日获得的总利润最大?
型游船才能使其当日获得的总利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若1路、2路公交车均途经泉港一中校门口,其中1路公交车每10分钟一趟,2路公交车每20分钟一趟,某生去坐这2趟公交车回家,则等车不超过5分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆C:![]() 的离心率为
的离心率为![]() ,连接椭圆四个顶点形成的四边形面积为4
,连接椭圆四个顶点形成的四边形面积为4![]() .
.
(1)求椭圆C的标准方程;
(2)过点A(1,0)的直线与椭圆C交于点M, N,设P为椭圆上一点,且![]() O为坐标原点,当
O为坐标原点,当![]() 时,求t的取值范围.
时,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com