解:(I)f(x)的定义域为{x|x>0},f′(x)=
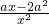
+1(x>0),
根据题意,有f′(1)=-2,
所以2a
2-a-3=0,解得a=-1或a=

.
(II)f′(x)=
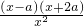
(x>0),
(1)当a>0时,因为x>0,
由f′(x)>0,得(x-a)(x+2a)>0,解得x>a;
由f′(x)<0得(x-a)(x+2a)<0,解得0<x<a.
所以函数f(x)在(a,+∞)上单调递增,在(0,a)上单调递减;
(2)当a<0时,因为x>0,
由f′(x)>0,得(x-a)(x+2a)>0,解得x>-2a;
由f′(x)<0,得(x-a)(x+2a)<0,解得0<x<-2a.
所以函数f(x)在(-2a,+∞)上单调递增,在(0,-2a)上单调递减;
(III)证明:由(Ⅱ)知,且g(a)=f(-2a)=aln(-2a)-3a,
∴g′(a)=ln(-2a)-2,
令g′(a)=0,得a=-

.
当a变化时,g′(a),g(a)的变化情况如下表:
| a | (-∞,- ) ) | - | (- ,0) ,0) |
| g′(a) | + | 0 | - |
| g(a) | 递增 | 极大值 | 递减 |
∴-

是g(a)在(-∞,0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点.
所以g(a)
max=g(-

)=-

ln[-2×(-

e
2)]-3(-

)=-

lne
2+

=

.
所以,当a∈(-∞,0)时,g(a)≤

成立.
分析:(I)确定f(x)的定义域,利用曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,可得f′(1)=-2,从而可求实数a的值;
(II)求导函数,分类讨论,利用导数的正负,即可确定函数f(x)的单调性;
(III)由(Ⅱ)知,当a∈(-∞,0)时,函数f(x)的最小值为g(a),且g(a)=f(-2a)=aln(-2a)-3a,求导数,求出函数的最大值,即可证得结论.
点评:本题考查导数知识的综合运用,考查函数的单调性、导数的几何意义及函数的最值问题,解题的关键是准确求导.

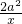 +x(a≠0).
+x(a≠0).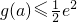 (e是自然对数的底数).
(e是自然对数的底数).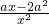 +1(x>0),
+1(x>0), .
.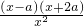 (x>0),
(x>0), .
. )
)
 ,0)
,0) 是g(a)在(-∞,0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点.
是g(a)在(-∞,0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点. )=-
)=- ln[-2×(-
ln[-2×(- e2)]-3(-
e2)]-3(- )=-
)=- lne2+
lne2+ =
= .
. 成立.
成立.
