
【题目】2018年10月19日,由中国工信部、江西省政府联合主办的世界VR(虚拟现实)产业大会在南昌开幕,南昌在红谷滩新区建立VR特色小镇项目.现某厂商抓住商机在去年用450万元购进一批VR设备,经调试后今年投入使用,计划第一年维修、保养费用22万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为180万元,设使用x年后设备的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,当年平均盈利额达到最大值时,求该厂商的盈利额.
科目:高中数学 来源: 题型:
【题目】某小区内有一块以![]() 为圆心半径为20米的圆形区域.广场,为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
为圆心半径为20米的圆形区域.广场,为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内且在圆
内且在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过60米.设
处的距离都不超过60米.设![]() .
.

(1)求![]() 的长(用
的长(用![]() 表示);
表示);
(2)对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(I)求函数在点(1,0)处的切线方程;
(II)设实数k使得f(x)< kx恒成立,求k的范围;
(III)设函数![]() ,求函数h(x)在区间
,求函数h(x)在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)上一点P(3,t)到其焦点的距离为4.
(1)求p的值;
(2)过点Q(1,0)作两条直线l1 , l2与抛物线分别交于点A、B和C、D,点M,N分别是线段AB和CD的中点,设直线l1 , l2的斜率分别为k1 , k2 , 若k1+k2=3,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项为an=log(n+1)(n+2)(n∈N*),我们把使乘积a1a2a3…an为整数的n叫做“优数”,则在(0,2015]内的所有“优数”的和为( )
A.1024
B.2012
C.2026
D.2036
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC=![]() BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
(1)证明:B1E∥平面ACF;
(2)求平面ADB1与平面ECB1所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(2x-x2)ex
①(-![]() ,
,![]() )是f(x)的单调递减区间;
)是f(x)的单调递减区间;
②f(-![]() )是f(x)的极小值,f(
)是f(x)的极小值,f(![]() )是f(x)的极大值;
)是f(x)的极大值;
③f(x)没有最大值,也没有最小值;
④f(x)有最大值,没有最小值.
其中判断正确的是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知摄影爱好者的身高约为
,已知摄影爱好者的身高约为![]() 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按![]() 米处理).
米处理).
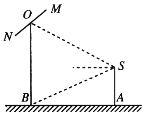
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB;
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角![]() (设为
(设为![]() )是否存在最大值?若存在,请求出
)是否存在最大值?若存在,请求出![]() 取最大值时
取最大值时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com