
【题目】设p:实数x满足![]() ,其中
,其中![]() ,命题
,命题![]() 实数
实数![]() 满足
满足
|x-3|≤1 .
(1)若![]() 且
且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]()
![]() 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。
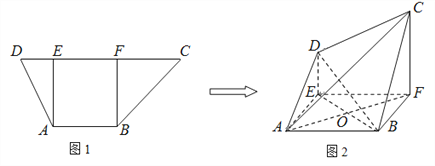
(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
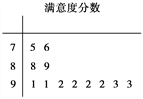
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是万物之本、生命之源,节约用水,从我做起.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
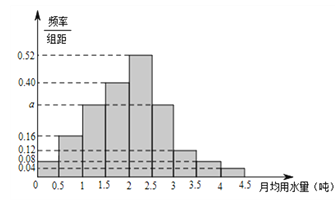
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数字0、2、3、4、6按下列要求组数、计算:
(1)能组成多少个没有重复数字的三位数?
(2)可以组成多少个可以被3整除的没有重复数字的三位数?
(3)求![]() 即144的所有正约数的和.
即144的所有正约数的和.
(注:每小题结果都写成数据形式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)延长![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作抛物线的切线
作抛物线的切线![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五面体![]() 中,
中,![]() ,底面
,底面![]() 是正三角形,
是正三角形,![]() ,四边形
,四边形![]() 是矩形,二面角
是矩形,二面角![]() 为直二面角.
为直二面角.
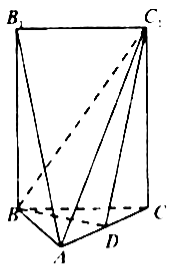
(1)![]() 在
在![]() 上运动,当
上运动,当![]() 在何处时,有
在何处时,有![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 余弦值.
余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
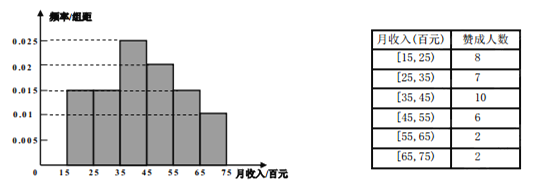
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 短轴顶点在圆
短轴顶点在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 方程;
方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究以
两点,试探究以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com