

 (1)证明:∵AB是圆柱ABFG的母线,C是点A关于点B对称的点,
(1)证明:∵AB是圆柱ABFG的母线,C是点A关于点B对称的点, ,(6分)
,(6分) ,(8分)
,(8分) ,即
,即 时“=”成立,(9分)
时“=”成立,(9分) ,即△BDE是等腰直角三角形 (10分)
,即△BDE是等腰直角三角形 (10分) ,
, ,∴
,∴
 ,∴
,∴ (13分)
(13分) ,即二面角C-DE-A的平面角的余弦值为0.(14分)
,即二面角C-DE-A的平面角的余弦值为0.(14分)

科目:高中数学 来源: 题型:
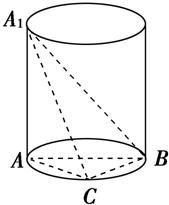 如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任=A意一点,A1A=AB=2.
如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任=A意一点,A1A=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:
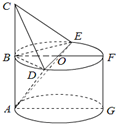 (2012•肇庆二模)如图,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.
(2012•肇庆二模)如图,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
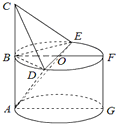 如图,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.
如图,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:BC⊥平面PAC;
(2)若C恰为弧![]() 的中点,按图中所给尺寸,计算三棱锥B—PAC的体积.
的中点,按图中所给尺寸,计算三棱锥B—PAC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com