
【题目】已知数列![]() 满足
满足![]() (
(![]() ),
),![]() (
(![]() ),则下列说法中错误的是( )
),则下列说法中错误的是( )
A.若![]() ,则数列
,则数列![]() 为递增数列
为递增数列
B.若数列![]() 为递增数列,则
为递增数列,则![]()
C.存在实数![]() ,使数列
,使数列![]() 为常数数列
为常数数列
D.存在实数![]() ,使
,使![]() 恒成立
恒成立
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】2017年9月支付宝宣布在肯德基的KPRO餐厅上线刷脸支付,也即用户可以不用手机,单单通过刷脸就可以完成支付宝支付,这也是刷脸支付在全球范围内的首次商用试点.某市随机抽查了每月用支付宝消费金额不超过3000元的男女顾客各300人,调查了他们的支付宝使用情况,得到如下频率分布直方图:
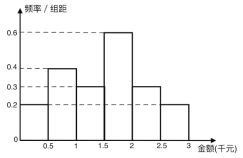
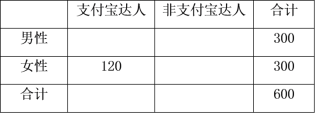
若每月利用支付宝支付金额超过2千元的顾客被称为“支付宝达人”, 利用支付宝支付金额不超过2千元的顾客称为“非支付宝达人”.
(I)若抽取的“支付宝达人”中女性占120人,请根据条件完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
(II)支付宝公司为了进一步了解这600人的支付宝使用体验情况和建议,从“非支付宝达人” “支付宝达人”中用分层抽样的方法抽取8人.若需从这8人中随机选取2人进行问卷调查,求至少有1人是“支付宝达人”的概率.
附:参考公式与参考数据如下
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷等比数列![]() 的首项、公比均为
的首项、公比均为![]() .
.
(1)试求无穷等比子数列![]() 各项的和;
各项的和;
(2)是否存在数列![]() 的一个无穷等比子数列,使得它各项的和为
的一个无穷等比子数列,使得它各项的和为![]() ?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 作动直线
作动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为平面上一点,直线
为平面上一点,直线![]() 的斜率分别为
的斜率分别为![]() ,且满足
,且满足![]() ,问
,问![]() 点是否在某定直线上运动,若存在,求出该直线方程;若不存在,请说明理由.
点是否在某定直线上运动,若存在,求出该直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
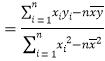 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高血压高血糖和高血脂统称“三高”.如图是西南某地区从2010年至2016年患“三高”人数y(单位:千人)的折线图.
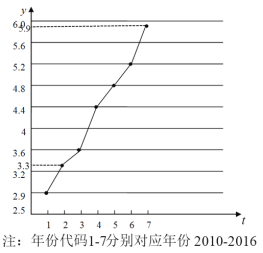
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请求出相关系数(精确到0.01)并加以说明;
的关系,请求出相关系数(精确到0.01)并加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测2018年该地区患“三高”的人数.
的回归方程,预测2018年该地区患“三高”的人数.
参考数据:![]() ,
,![]() ,
, ,
,![]() .
.
参考公式:相关系数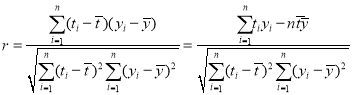 ,
,
回归方程![]() 中:
中: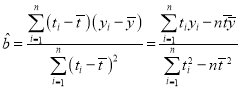 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com