
【题目】我国唐代天文学家、数学家张逐曾以“李白喝酒”为题编写了如下一道题:“李白街上走,提壶去买酒,遇店加一倍,见花喝一斗(计量单位),三遇店和花,喝光壶中酒.”问最后一次遇花时有酒________斗,原有酒________斗.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )
A.3233万元B.4706万元C.4709万元D.4808万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,以
,以![]() 为圆心过椭圆左顶点
为圆心过椭圆左顶点![]() 的圆与直线
的圆与直线![]() 相切于
相切于![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,问
,问![]() 内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
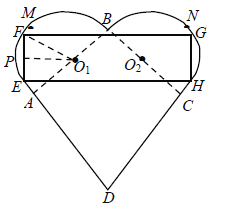
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
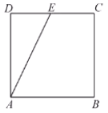
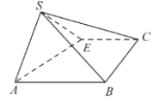
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() x∈R,其中a,b∈R.
x∈R,其中a,b∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0,且f(x1)= f(x0),其中x1≠x0,求证:x1+2x0=3;
(Ⅲ)设a>0,函数g(x)= |f(x)|,求证:g(x)在区间[0,2]上的最大值不小于![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com