
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.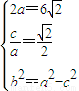 解之即得a,b,从而写出所求椭圆M的方程;
解之即得a,b,从而写出所求椭圆M的方程;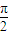 ,设直线AB的斜率为k=tanθ,焦点F ( 3,0 ),则直线AB的方程为y=k ( x-3 ),将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得|AB|+|CD|的最小值,从而解决问题.
,设直线AB的斜率为k=tanθ,焦点F ( 3,0 ),则直线AB的方程为y=k ( x-3 ),将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得|AB|+|CD|的最小值,从而解决问题.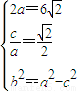 ⇒
⇒ 所求椭圆M的方程为
所求椭圆M的方程为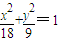 …(3分)
…(3分)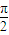 ,设直线AB的斜率为k=tanθ,焦点F ( 3,0 ),则直线AB的方程为y=k ( x-3 )有
,设直线AB的斜率为k=tanθ,焦点F ( 3,0 ),则直线AB的方程为y=k ( x-3 )有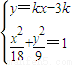 ⇒( 1+2k2 )x2-12k2x+18( k2-1 )=0
⇒( 1+2k2 )x2-12k2x+18( k2-1 )=0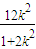 ,x1x2=
,x1x2=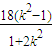

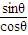 代入**式得|AB|=
代入**式得|AB|=
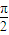 时,直线AB的方程为x=3,此时|AB|=
时,直线AB的方程为x=3,此时|AB|=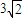
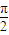 时,|AB|=
时,|AB|= =
=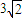
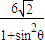
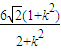 =
=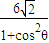
 +
+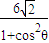 =
=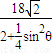
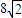


科目:高中数学 来源:2008-2009学年湖北省天门中学高二(下)5月月考数学试卷(A卷)(解析版) 题型:解答题
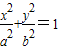 (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点. ;
;查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省徐州七中高考数学模拟试卷(解析版) 题型:解答题
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,长轴长为
,长轴长为 ,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点.
,设过右焦点F倾斜角为θ的直线交椭圆M于A,B两点. ;
;查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省四校高三第二次联考数学试卷(文科)(解析版) 题型:解答题
 (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.查看答案和解析>>
科目:高中数学 来源:2011年山东省高考数学仿真押题试卷01(文科)(解析版) 题型:解答题
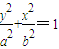 (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4.
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4. x+m交椭圆于A、B两点,椭圆上一点
x+m交椭圆于A、B两点,椭圆上一点 ,求△PAB面积的最大值.
,求△PAB面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com