
| A. | -$\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$或-$\frac{4}{9}$ | D. | -$\frac{2}{9}$或$\frac{4}{9}$ |
分析 根据向量的加减的几何意义和向量的数量积公式计算即可.
解答 解:M是BC上的第一个三等分点,则$\overrightarrow{MA}$•$\overrightarrow{MB}$=($\overrightarrow{MB}$+$\overrightarrow{BA}$)$\overrightarrow{MB}$=($\frac{1}{3}$$\overrightarrow{CB}$+$\overrightarrow{BA}$)•$\frac{1}{3}$$\overrightarrow{CB}$=$\frac{1}{9}$${\overrightarrow{CB}}^{2}$-$\frac{1}{3}$$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\frac{1}{9}$×22-$\frac{1}{3}$×2×2cos60°=-$\frac{2}{9}$,
故选:A
点评 本题考查了向量的加减的几何意义和向量的数量积公式,属于基础题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:选择题
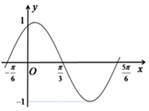 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象.为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象.为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上所有的点( )| A. | 向左平移$\frac{π}{3}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| B. | 向左平移$\frac{π}{3}$个单位,再把所得各点的横坐标伸长到原来的2倍 | |
| C. | 向左平移$\frac{π}{6}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| D. | 向左平移$\frac{π}{6}$个单位,再把所得各点的横坐标伸长到原来的2倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
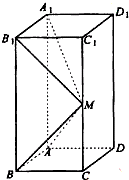 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,4} | B. | {-4,0} | C. | {-4,0,4} | D. | {0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com