解答:解:(1)(3-p)S
n+2pa
n=3+p,p为常数,且p<-3,n∈N*.
所以(3-p)S
n-1+2pa
n-1=3+p,(n≥2),两式相减得:(3-p)a
n+2pa
n-2pa
n-1=0 (n≥2)
即:(3+p)a
n=2pa
n-1 (n≥2),所以
=(n≥2)--------------------------2分
当n=1时,(3-p)a
1+2pa
1=3+p,a
1=1,故数列{a
n}是等比数列-----------------------2分
a
n=(
)
n-1--------------------------------------------2分
(2)数列{a
n}的公比q=f(p),q=f(p)=
,b
1=a
1,b
n=
f(b
n-1),(n≥2),
所以b
n=
?
=
,所以
=
=
+
,
-=
,b
1=a
1=1------------------3分
数列{
}是等差数列,
=1+
(n-1)=
,所以b
n=
;----------------2分
(3)因为a
n-a
n+1=(
)
n-1-(
)
n=(
)
n-1[1-
]=
()n-1由
cn==
()n-1因为lga
n=lg(
)
n-1=(n-1)lg
,
b
nlga
n=
lg
(b
nlga
n)=
[
lg
]=3lg
因为
(bnlgan)=lg27,所以
3lg=lg27,p=-9----------------3分
所以c
n=-
(
)
n-1,故{c
n}的各项和为S=
=-
.----------------2分.



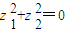 ,则z1=0且z2=0;
,则z1=0且z2=0;