
【题目】如图,在![]() 中,
中,![]() ,斜边
,斜边![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角,动点
是直二面角,动点![]() 在斜边
在斜边![]() 上.
上.
(1)当D为AB的中点时,求异面直线AO与CD所成角的正切值;
(2)求CD与平面AOB所成角的正切值的最大值.

【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)求异面直线所成的角,需要将两条异面直线平移交于一点,由![]() 为
为![]() 的中点,故平移时很容易应联想中位线,作
的中点,故平移时很容易应联想中位线,作![]() ,垂足为
,垂足为![]() 连接
连接![]() ,则
,则![]() ,
,![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角,利用解三角形的有关知识夹角问题即可;(2)本题的设问是递进式的,求直线与平面所成的角,
所成的角,利用解三角形的有关知识夹角问题即可;(2)本题的设问是递进式的,求直线与平面所成的角,![]() 是
是![]() 与平面
与平面![]() 所成角,
所成角,
![]() ,当
,当![]() 最小时,
最小时,![]() 最大.
最大.
(1)作DE⊥OB,垂足为E,连接CE,所以DE∥AO,
∴∠CDE(或其补角)是异面直线AO与CD所成的角.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
又![]() ,所以
,所以![]() ,
,
∴在![]() 中,
中,![]() ,
,
所以异面直线AO与CD所成角的余弦值大小为![]() .
.
(2)由(1)知,![]() 平面
平面![]() ,
,
∴![]() 是
是![]() 与平面
与平面![]() 所成的角,并且
所成的角,并且![]() ,
,
当![]() 最小时,
最小时,![]() 最大,这时,
最大,这时,![]() ,垂足为
,垂足为![]() ,
,
所以![]() ,∴
,∴![]() ,
,
所以![]() 与平面
与平面![]() 所成的角的最大时的正切值为
所成的角的最大时的正切值为![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1 , A2 , A3 , A4 , A5 , A6和4名女志愿者B1 , B2 , B3 , B4 , 从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(12分)
(Ⅰ)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在复平面内对应的点在第一象限,且z=-3+4i.
(1)求z2及|z2|.
(2)若z1=z2,求θ与a2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小张的投篮命中率与打篮球时间之间的关系,下表记录了小张某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(1)求小张这![]() 天的平均投篮命中率;
天的平均投篮命中率;
(2)利用所给数据求小张每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的线性回归方程
之间的线性回归方程![]() ;(参考公式:
;(参考公式:![]() )
)
(3)用线性回归分析的方法,预测小李该月![]() 号打
号打![]() 小时篮球的投篮命中率.
小时篮球的投篮命中率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.
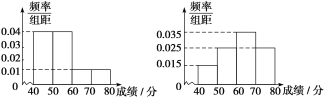
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)若称成绩在68分以上的学生知识渊博,试以上述数据估计该高一、高二两个年级学生的知识渊博率;
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.
分类 | 成绩低于60分人数 | 成绩不低于60分人数 | 总计 |
高一年级 | |||
高二年级 | |||
总计 |
附:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对![]() 岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图:
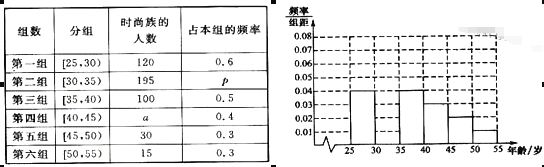
完成以下问题:
(Ⅰ)补全频率分布直方图并求![]() 的值;
的值;
(Ⅱ)从![]() 岁年龄段的“时尚族”中采用分层抽样法抽取
岁年龄段的“时尚族”中采用分层抽样法抽取![]() 人参加网络时尚达人大赛,其中选取
人参加网络时尚达人大赛,其中选取![]() 人作为领队,记选取的
人作为领队,记选取的![]() 名领队中年龄在
名领队中年龄在![]() 岁的人数为
岁的人数为![]() ,求
,求![]() 的分布列
的分布列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列题目的证法,再解决后面的问题.
已知a1,a2∈R,且a1+a2=1,求证:a+a≥![]() .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a+a=2x2-2x+a+a.
因为对一切x∈R,恒有f(x)≥0,
所以Δ=4-8(a+a)≤0,从而得a+a≥![]() .
.
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请由上述结论写出关于a1,a2,…,an的推广式;
(2)参考上述证法,请对你推广的结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com