
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)证明:不等式![]() 对于正整数
对于正整数![]() 恒成立,其中
恒成立,其中![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)第(1)问,方法一,构造函数![]() ,再分析f(x)的最大值和零的关系得到a的取值范围.方法二,分离参数得到
,再分析f(x)的最大值和零的关系得到a的取值范围.方法二,分离参数得到![]() 恒成立,即a大于F(x)的最大值. (2)第(2)问,先要把证明的不等式转化,再由第(1)问,
恒成立,即a大于F(x)的最大值. (2)第(2)问,先要把证明的不等式转化,再由第(1)问,![]() 恒成立,得到
恒成立,得到![]() 恒成立,把数列的通项放缩,对数列求和,再化简证明不等式.
恒成立,把数列的通项放缩,对数列求和,再化简证明不等式.
试题解析:
(1)法一:记![]() ,
,
则![]() ,
,![]() ,
,
①当![]() 时,
时,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上单减,
上单减,
又![]() ,∴
,∴![]() ,即
,即![]() 在
在![]() 上单减,
上单减,
此时,![]() ,即
,即![]() ,所以a≥1.
,所以a≥1.
②当![]() 时,
时,
考虑![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单增,
上单增,
又![]() ,∴
,∴![]() ,即
,即![]() 在
在![]() 上单増,
上单増,![]() ,不满足题意.
,不满足题意.
综上所述,![]() .
.
法二:当![]() 时,
时,![]() 等价于
等价于![]() ,
,
![]() ,记
,记![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单减,∴
上单减,∴![]() ,
,
∴![]() ,即
,即![]() 在
在![]() 上单减,
上单减,![]() ,故
,故![]() .
.
(2)由(1)知:取![]() ,当
,当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
即![]() 对于
对于![]() 恒成立,
恒成立,
由此,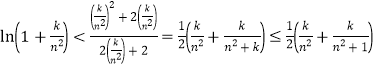 ,
,![]() ,
,
于是![]()
![]()
![]()
![]() ,
,
故![]() .
.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】有下列说法
①互斥事件不一定是对立事件,对立事件一定是互斥事件
②演绎推理是从特殊到一般的推理,它的一般模式是“三段论”
③残差图的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高
④若![]() ,则事件
,则事件![]() 与
与![]() 互斥且对立
互斥且对立
⑤甲乙两艘轮船都要在某个泊位停靠4小时,假定它们在一昼夜的时间段中随机到达,则这两艘船中至少有一艘在停靠泊位时必须等待的概率为![]() .
.
其中正确的说法是______(写出全部正确说法的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() =1(a>b>0)的右焦点为F(2,0),且过点(2
=1(a>b>0)的右焦点为F(2,0),且过点(2![]() ,
,![]() ).
).
(1)求椭圆的标准方程;
(2)设直线l:y=kx(k>0)与椭圆在第一象限的交点为M,过点F且斜率为-1的直线与l交于点N,若![]() sin∠FON(O为坐标原点),求k的值.
sin∠FON(O为坐标原点),求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题,
①双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
②在平面内,设![]() 为两个定点,
为两个定点,![]() 为动点,且
为动点,且![]() ,其中常数
,其中常数![]() 为正实数,则动点
为正实数,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
③方程![]() 的两根可以分别作为椭圆和双曲线的离心率;
的两根可以分别作为椭圆和双曲线的离心率;
④过双曲线![]() 的右焦点
的右焦点![]() 作直线
作直线![]() 交双曲线于
交双曲线于![]() 两点,若
两点,若![]() ,则这样的直线
,则这样的直线![]() 有且仅有3条.
有且仅有3条.
其中真命题的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
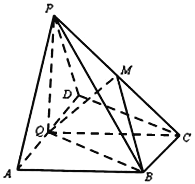
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是______米(精确到0.1米)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列判断正确的是()
对称,则下列判断正确的是()
A. 函数![]() 在
在![]() 上单调递增
上单调递增
B. 函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
C. 当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
D. 要得到函数![]() 的图像,只需要
的图像,只需要![]() 将的图像向右平移
将的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黒球的口袋内任取
个黒球的口袋内任取![]() 个球,则互为对立事件是( )
个球,则互为对立事件是( )
A. 至少有一个黒球与都是黒球B. 至少有一个黒球与都是红球
C. 至少有一个黒球与至少有![]() 个红球D. 恰有
个红球D. 恰有![]() 个黒球与恰有
个黒球与恰有![]() 个黒球
个黒球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养殖的水产品在临近收获时,工人随机从水中捕捞![]() 只,其质量分别在
只,其质量分别在![]()
![]() (单位:克),经统计分布直方图如图所示.
(单位:克),经统计分布直方图如图所示.

(1)求这组数据的众数;
(2)现按分层抽样从质量为![]() 的水产品种随机抽取
的水产品种随机抽取![]() 只,在从这
只,在从这![]() 只中随机抽取
只中随机抽取![]() 只,求这
只,求这![]() 只水产品恰有
只水产品恰有![]() 只在
只在![]() 内的概率;
内的概率;
(3)某经销商来收购水产品时,该养殖场现还有水产品共计约![]() 只要出售,经销商提出如下两种方案:
只要出售,经销商提出如下两种方案:
方案A:所有水产品以![]() 元/只收购;
元/只收购;
方案B:对于质量低于![]() 克的水产品以
克的水产品以![]() 元/只收购,不低于
元/只收购,不低于![]() 克的以
克的以![]() 元/只收购,
元/只收购,
通过计算确定养殖场选择哪种方案获利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com