
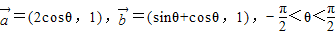
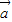 ∥
∥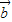 ,求θ的值
,求θ的值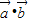 ,求函数f(θ)的最大值及单调递增区间.
,求函数f(θ)的最大值及单调递增区间.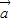 ∥
∥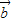 ,,可得sinθ=cosθ,由此得tanθ=1,再由
,,可得sinθ=cosθ,由此得tanθ=1,再由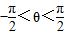 ,即可判断出θ的值;
,即可判断出θ的值;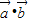 及两向量的坐标得到f(θ)的函数解析式,再由三角函数的最值的判断出函数的最值,利用正弦函数的单调性求出函数的单调递增区间.
及两向量的坐标得到f(θ)的函数解析式,再由三角函数的最值的判断出函数的最值,利用正弦函数的单调性求出函数的单调递增区间.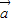 ∥
∥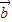 ,,可得sinθ=cosθ,由此得tanθ=1,又
,,可得sinθ=cosθ,由此得tanθ=1,又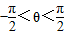 ,故有θ=
,故有θ=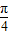
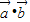 =2sinθcosθ+2cos2θ+1=sin2θ+cos2θ+2=
=2sinθcosθ+2cos2θ+1=sin2θ+cos2θ+2=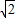 sin(2θ+
sin(2θ+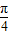 )+2
)+2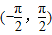 ,所以2θ+
,所以2θ+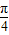 ∈
∈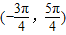
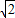 +2,
+2,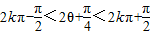
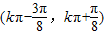
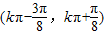


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com