
【题目】已知抛物线![]() :
:![]() (
(![]() ),圆
),圆![]() :
:![]() (
(![]() ),抛物线
),抛物线![]() 上的点到其准线的距离的最小值为
上的点到其准线的距离的最小值为![]() .
.
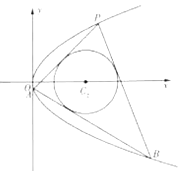
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(2)如图,点![]() 是抛物线
是抛物线![]() 在第一象限内一点,过点P作圆
在第一象限内一点,过点P作圆![]() 的两条切线分别交抛物线
的两条切线分别交抛物线![]() 于点A,B(A,B异于点P),问是否存在圆
于点A,B(A,B异于点P),问是否存在圆![]() 使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3.
(1)求椭圆C的标准方程;
(2)过点P(0,1)的直线l与椭圆C交于两点A,B.己知在椭圆C上存在点Q,使得四边形OAQB是平行四边形,求Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线与抛物线交于A,B两点,又过A,B两点分作抛物线的切线,两条切线交于P点.记直线PA、PB的斜率分别为
的直线与抛物线交于A,B两点,又过A,B两点分作抛物线的切线,两条切线交于P点.记直线PA、PB的斜率分别为![]() 和
和![]() .
.
(1)求![]() 的值;
的值;
(2)![]() ,
,![]() ,求四边形PAEG面积的最小值.
,求四边形PAEG面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图平面PAC⊥平面ABC, AC⊥BC,PE// BC,M,N分别是AE,AP的中点,且△PAC是边长为2的等边三角形,BC=3,PE =2.

(1)求证:MN⊥平面PAC;
(2)求平面PAE与平面ABC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() 的各项均为整数,它们的前
的各项均为整数,它们的前![]() 项和分别为
项和分别为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)求![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 恰好是数列
恰好是数列![]() 或
或![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB![]() ,平面α过长方体顶点D,且平面α∥平面AB1C,平面α∩平面ABB1A1=l,则直线l与BC1所成角的余弦值为( )
,平面α过长方体顶点D,且平面α∥平面AB1C,平面α∩平面ABB1A1=l,则直线l与BC1所成角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三年级学生在线学习情况,统计了2020年2月18日-27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.
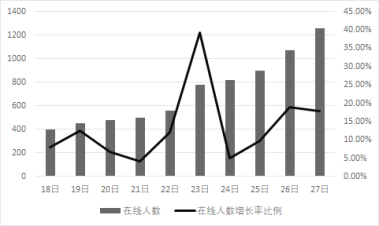
根据组合图判断,下列结论正确的是( )
A.前5天在线学习人数的方差大于后5天在线学习人数的方差
B.前5天在线学习人数的增长比例的极差大于后5天的在线学习人数的增长比例的极差
C.这10天学生在线学习人数的增长比例在逐日增大
D.这10天学生在线学习人数在逐日增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),椭圆上的点到焦点的最小距离为
1(a>b>0),椭圆上的点到焦点的最小距离为![]() 且过点P(
且过点P(![]() ,1).
,1).
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线l与椭圆C有两个不同的交点P和Q,若点P关于x轴的对称点为P',判断直线P'Q是否经过定点,如果经过,求出该定点坐标;如果不经过,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com