
【题目】已知函数![]() ,集合
,集合![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,若函数
时,若函数![]() 的定义域为
的定义域为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 的值域为
的值域为![]() ;
;
当![]() 时,
时,![]() 的值域为
的值域为![]() ;当
;当![]() 时,
时,![]() 的值域为
的值域为![]() .
.
【解析】分析:(1)先根据一元二次方程解得ex>3,再解对数不等式得解集,(2)解一元二次不等式得集合A,再根据![]() ,得log2f(x)≥1在0≤x≤1上有解,利用变量分离法得a≥3ex-e2x在0≤x≤1上有解,即a≥[3ex-e2x]min.最后根据二次函数性质求最值得结果,(3)先转化为对勾函数,再根据拐点与定义区间位置关系,分类讨论,结合单调性确定函数值域.
,得log2f(x)≥1在0≤x≤1上有解,利用变量分离法得a≥3ex-e2x在0≤x≤1上有解,即a≥[3ex-e2x]min.最后根据二次函数性质求最值得结果,(3)先转化为对勾函数,再根据拐点与定义区间位置关系,分类讨论,结合单调性确定函数值域.
详解:(1)当a=-3时,由f(x)>1得ex-3e-x-1>1,
所以e2x-2ex-3>0,即(ex-3) (ex+1)>0,
所以ex>3,故x>ln3,
所以不等式的解集为(ln3,+∞).
(2)由x2-x≤0,得0≤x≤1,所以A={x|0≤x≤1}.
因为A∩B≠,所以log2f(x)≥1在0≤x≤1上有解,
即 f(x)≥2在0≤x≤1上有解,
即ex+ae-x-3≥0在0≤x≤1上有解,
所以a≥3ex-e2x在0≤x≤1上有解,即a≥[3ex-e2x]min.
由0≤x≤1得1≤ex≤e,
所以3ex-e2x=-(ex-![]() )2+
)2+![]() ∈[3e-e2,
∈[3e-e2,![]() ],
],
所以a≥3e-e2.
(3)设t=ex,由(2)知1≤t≤e,
记g(t)=t+![]() -1(1≤t≤e,a>1),则
-1(1≤t≤e,a>1),则![]() ,
,
t | (1, |
| ( |
g′(t) | - | 0 | + |
g(t) | ↘ | 极小值 | ↗ |
①当![]() ≥e时,即a≥e2时,
≥e时,即a≥e2时,
g(t)在1≤t≤e上递减,所以g(e)≤g(t)≤g(1),即![]() .
.
所以f(x)的值域为![]() .
.
②当1<![]() <e时,即1<a<e2时,
<e时,即1<a<e2时,
g(t)min= g(![]() )=2
)=2![]() -1,g(t)max=max{ g(1),g(e)} =max{ a,
-1,g(t)max=max{ g(1),g(e)} =max{ a,![]() }.
}.
1°若a![]() ,即e<a<e2时,g(t)max= g(1)= a;
,即e<a<e2时,g(t)max= g(1)= a;
所以f(x)的值域为![]() ;
;
2°若a![]() ,即1<a≤e时,g(t)max= g(e) =
,即1<a≤e时,g(t)max= g(e) =![]() ,
,
所以f(x)的值域为![]() .
.
综上所述,当1<a≤e时,f(x)的值域为![]() ;
;
当e<a<e2时,f(x)的值域为![]() ;
;
当a≥e2时,f(x)的值域为![]() .
.


科目:高中数学 来源: 题型:
【题目】某项“过关游戏”规则规定:在地![]() 关要抛掷
关要抛掷![]() 颗骰子
颗骰子![]() 次,如果这
次,如果这![]() 次抛掷所出现的点数和大于
次抛掷所出现的点数和大于![]() ,则算过关.
,则算过关.
(Ⅰ)此游戏最多能过__________关.
(Ⅱ)连续通过第![]() 关、第
关、第![]() 关的概率是__________.
关的概率是__________.
(Ⅲ)若直接挑战第![]() 关,则通关的概率是__________.
关,则通关的概率是__________.
(Ⅳ)若直接挑战第![]() 关,则通关的概率是__________.
关,则通关的概率是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2, 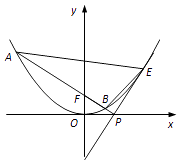
(1)求抛物线的方程;
(2)如图,点E是抛物线上异于原点的点,抛物线在点E处的切线与x轴相交于点P,直线PF与抛物线相交于A,B两点,求△EAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 函数
函数![]() 是
是![]() 上的奇函数,命题
上的奇函数,命题![]() 函数
函数![]() 的定义域和值域都是
的定义域和值域都是![]() ,其中
,其中![]() .
.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的值;
的值;
(2)若“![]() 且
且![]() ”为假命题,“
”为假命题,“![]() 或
或![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小陈同学进行三次定点投篮测试,已知第一次投篮命中的概率为![]() ,第二次投篮命中的概率为
,第二次投篮命中的概率为![]() ,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为
,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为![]() ,否则为
,否则为![]() .
.
(1)求小陈同学三次投篮至少命中一次的概率;
(2)记小陈同学三次投篮命中的次数为随机变量![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
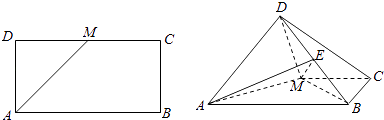
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的虚轴长为
的虚轴长为![]() ,两条渐近线方程为
,两条渐近线方程为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)双曲线![]() 上有两个点
上有两个点![]() ,直线
,直线![]() 和
和![]() 的斜率之积为
的斜率之积为![]() ,判别
,判别![]() 是否为定值,;
是否为定值,;
(3)经过点![]() 的直线
的直线![]() 且与双曲线
且与双曲线![]() 有两个交点
有两个交点![]() ,直线
,直线![]() 的倾斜角是
的倾斜角是![]() ,是否存在直线
,是否存在直线![]() (其中
(其中![]() )使得
)使得![]() 恒成立?(其中
恒成立?(其中![]() 分别是点
分别是点![]() 到
到![]() 的距离)若存在,求出
的距离)若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
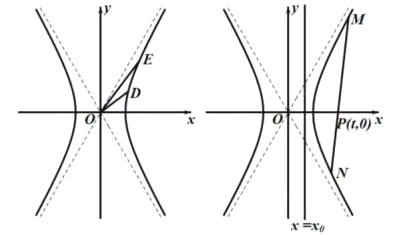
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .若存在,求出点P的位置;若不存在,说明理由.
.若存在,求出点P的位置;若不存在,说明理由.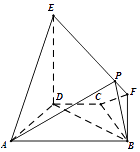
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com