练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （理） 空间三点A（0，1，0），B（2，2，0），C（-1，3，1），则（　　）
    分析：A：根据题意两个向量的坐标表示，可得
    AB
    分别写出
    AB
    ≠λ
    AC
    ，所以
    AB
    与
    AC
    不共线．
    B：结合题意可得：
    AB
    的单位向量为：(
    2
    		5
    5
    ，
    		5
    5
    ，0)    或(-
    2
    		5
    5
    ，-
    		5
    5
    ，0)    ．
    C：根据题意分别写出两个向量的坐标表示，再结合向量的数量积公式求出两个向量夹角的余弦值．
    D：设平面ABC的一个法向量是
    n
    =(x，y，z)    ，利用
    AB
    •
    n
    =0
    AC
    •
    n
    =0
    ，可得x：y：z=1：（-2）：5．
    解答：解：A：
    AB
    =（2，1，0），
    AC
    =（-1，2，1），所以
    AB
    ≠λ
    AC
    ，所以
    AB
    与
    AC
    不共线，所以A错误．
    B：因为
    AB
    =（2，1，0），所以
    AB
    的单位向量为：(
    2
    		5
    5
    ，
    		5
    5
    ，0)    或(-
    2
    		5
    5
    ，-
    		5
    5
    ，0)    ，所以B错误．
    C：
    AB
    =（2，1，0），
    BC
    =(-3，1，1)    ，所以cos＜
    AB
    ，
    BC
    ＞    =
    AB
    •
    BC
    |
    AB
    |  |
    BC
    |
    =-
    		55
    11
    ，所以C错误．
    D：设平面ABC的一个法向量是
    n
    =(x，y，z)    ，因为
    AB
    =（2，1，0），
    AC
    =（-1，2，1），所以
    AB
    •
    n
    =0
    AC
    •
    n
    =0
    ，即
    2x+y=0
    -x+2y+z=0
    ，所以x：y：z=1：（-2）：5，所以D正确．
    故选D．
    点评：本题主要考查向量之间的运算，即向量坐标形式的数量积运算、向量坐标形式的共线与利用向量的数量积运算求平面的法向量．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （文做理不做）正方体ABCD-A1B1C1D1中，p、q、r分别是AB、AD、B1C1的中点．那么正方体的过P、Q、R的截面图形是
    正六边形
    正六边形
    ．
    （理做文不做）已知空间三个点A（-2，0，2）、B（-1，1，2）和C（-3，0，4），设
    a
    =
    AB
    ，
    b
    =
    AC
    ．当实数k为
    k=-
    5
    2
    或k=2
    k=-
    5
    2
    或k=2
    时k
    a
    +
    b
    与k
    a
    -2
    b
    互相垂直．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    （理） 空间三点A（0，1，0），B（2，2，0），C（-1，3，1），则


    1. A.
      数学公式与数学公式是共线向量
    2. B.
      数学公式的单位向量是（1，1，0）
    3. C.
      数学公式与数学公式夹角的余弦值数学公式
    4. D.
      平面ABC的一个法向量是（1，-2，5）

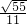
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    （理） 空间三点A（0，1，0），B（2，2，0），C（-1，3，1），则（　　）
    A．
    AB
    与
    AC
    是共线向量
    B．
    AB
    的单位向量是（1，1，0）
    C．
    AB
    与
    BC
    夹角的余弦值
    		55
    11
    D．平面ABC的一个法向量是（1，-2，5）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年滨州市质检三理） 在空间中，有如下命题：

        ①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线；

        ②若平面；

        ③若平面；

        ④若平面内的三点A、B、C到平面的距离相等，则.

        其中正确命题的个数为（    ）个。                                    （    ）

        A．0              B．1              C．2              D．3

    查看答案和解析>>

    同步练习册答案