练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    给出问题：已知满足，试判定的形状.某学生的解答如下：

    解：（i）由余弦定理可得，

    ，

    ，

    ,

    故是直角三角形.

    （ii）设外接圆半径为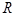.由正弦定理可得，原式等价于

    ，

    故是等腰三角形.

    综上可知，是等腰直角三角形.

    请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果.　　    　　　　　.

     

    【答案】

    等腰或直角三角形

    【解析】解：第一种解法中，两边同时约分，造成了方程丢解，那就是等腰三角形

    第二种解法中，由于正弦值相等，可能A=B，也可能A+B=

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•普陀区一模）给出问题：已知△ABC满足a•cosA=b•cosB，试判断△ABC的形状，某学生的解答如下：
    （i）a•
    b2+c2-a2
    2bc
    =b•
    a2+c2-b2
    2ac
    ?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2
    故△ABC是直角三角形．
    （ii）设△ABC外接圆半径为R，由正弦定理可得，原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
    故△ABC是等腰三角形．
    综上可知，△ABC是等腰直角三角形．
    请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果
    等腰或直角三角形
    等腰或直角三角形
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    给出问题：已知△ABC满足a•cosA=b•cosB，试判断△ABC的形状，某学生的解答如下：
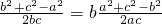    （i）a•数学公式?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2
    故△ABC是直角三角形．
    （ii）设△ABC外接圆半径为R，由正弦定理可得，原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
    故△ABC是等腰三角形．
    综上可知，△ABC是等腰直角三角形．
    请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果________．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市普陀区高考数学一模试卷（文科）（解析版） 题型：解答题

    给出问题：已知△ABC满足a•cosA=b•cosB，试判断△ABC的形状，某学生的解答如下：
    （i）a•?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2
    故△ABC是直角三角形．
    （ii）设△ABC外接圆半径为R，由正弦定理可得，原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
    故△ABC是等腰三角形．
    综上可知，△ABC是等腰直角三角形．
    请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果    ．

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市普陀区高考数学一模试卷（理科）（解析版） 题型：解答题

    给出问题：已知△ABC满足a•cosA=b•cosB，试判断△ABC的形状，某学生的解答如下：
    （i）a•?a2（b2+c2-a2）=b2（a2+c2-b2）?（a2-b2）•c2=（a2-b2）（a2+b2）?c2=a2+b2
    故△ABC是直角三角形．
    （ii）设△ABC外接圆半径为R，由正弦定理可得，原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
    故△ABC是等腰三角形．
    综上可知，△ABC是等腰直角三角形．
    请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果    ．

    查看答案和解析>>

    同步练习册答案