
如图a所示,正△ABC的边长为2![]() ,CD是AB边上的高,E、F分别是AC和BC边的中点.现将△ABC沿CD翻折成直二面角A―DC―B,如图b所示.
,CD是AB边上的高,E、F分别是AC和BC边的中点.现将△ABC沿CD翻折成直二面角A―DC―B,如图b所示.

(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角B―AC―D的大小;
(3)求点C到平面DEF的距离.
解法一:(1)在△ABC中,∵E、F分为AC、BC中点.∴EF//AB。
又AB![]() 平面DEF,EF
平面DEF,EF![]() 平面DEF,∴AB∥平面DEF.
平面DEF,∴AB∥平面DEF.
(2)过D作DG⊥AC于G,连接BG.

∵AD⊥CD,BD⊥CE,
∴∠ADB是二面角A―CD―B的平面角.
∴∠ADB=90°,即BD⊥AD.
∴BD⊥平面ADC.∴BG⊥AC.
∴∠BGD是二面角B―AC―D的平面角
在Rt△ADC中,AD=![]() ,BC=
,BC=![]() ,AC=2
,AC=2![]() .
.
∴DG=![]() .
.
在Rt△BDG中,tan∠BGD=![]()
∴∠BGD=arctan![]() .
.
即二面角B―AC―D的大小为arctan![]() .
.
(3)过E作EH⊥DC于H.
∵BD⊥平面ADC,又EH![]() 平面ADC,
平面ADC,
∴BD⊥EH,∴EH⊥平面BCD.
∵EH=![]() AD=
AD=![]() ,S△CDF=
,S△CDF=![]() S△BCD=
S△BCD=![]() ,
,
cos∠EDF=![]() ,
,
sin∠EDF=![]() .
.
S△DEF=![]() DE?DF?sin∠EDF=
DE?DF?sin∠EDF=![]() .
.
设点C到平面DEF的距离为h.
∴VC-DEF=VE-CDF,
∴![]() ,
,
即![]() ,
,![]() .故点C到平面DEF的距离为
.故点C到平面DEF的距离为![]() .
.
解法二:(1)如图所示,建立空间直角坐标系O―![]() ,
,

则D(0,0,0),A(0,0,![]() ),B(
),B(![]() ,0,0),
,0,0),
C(0,![]() ,0),E(0,
,0),E(0,![]() ,
,![]() ),F(
),F(![]() ,
,![]() ,0),
,0),
∴![]() ,
,![]() .
.
∴![]() ,∴
,∴![]()
∴AB//EF,且EF![]() 平面DEF.
平面DEF.
∴AB∥平面DEF.
(2)∵![]() 为平面ACD的一个法向量,
为平面ACD的一个法向量,
设n=(![]() ,
,![]() ,z)为平面ABC的一个法向量,则
,z)为平面ABC的一个法向量,则
 ,取
,取![]() ,
,![]()
∴n=(1,![]() ,1)
,1)
∴ .
.
∴二面角B―AC―D的大小为![]() .
.
(3)设m=(![]() ,
,![]() ,z)为平面DFE的一个法向量,则
,z)为平面DFE的一个法向量,则

取![]() =1,则
=1,则![]() .
.
∴m=(![]() ,1,
,1,![]() ).
).
![]()
∴点C到平面DEF的距离为
d=![]()
=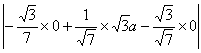
=![]()


科目:高中数学 来源:山东省潍坊市2012届高考考前适应性训练(三模)数学理科试题 题型:013
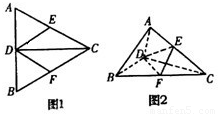
如图1所示,正△ABC中,CD是AB边上的高,E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面ACD⊥平面BCD(如图2),则下列结论中不正确的是
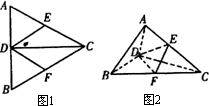
A.AB∥平面DEF
B.CD⊥平面ABD
C.EF⊥平面ACD
D.V三棱锥C-ABD=4V三棱锥C-DEF
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三上学期第三次统练理科数学试卷(解析版) 题型:选择题
如图1所示,正△ABC中,CD是AB边上的高, E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )
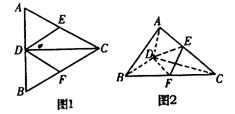
A.AB//平面DEF B.CD⊥平面ABD
C.EF⊥平面ACD D.V三棱锥C—ABD=4V三棱锥C—DEF
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求曲线C的方程;
(2)已知点A(5,0)、B(1,0),过点A作直线交曲线C于两个不同的点P、Q,△BPQ的面积S是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
(文)如图b所示,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A,B到x轴距离之积为2m,以x轴为对称轴、过A,O,B三点作抛物线.
(1)求抛物线方程;
(2)若tan∠AOB=-1,求m的取值范围.
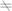
第21题图
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省莱芜市凤城高中高三(上)第三次质量检测数学试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com