
点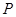 在正方体
在正方体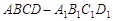 的面对角线
的面对角线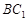 上运动,则下列四个命题:
上运动,则下列四个命题: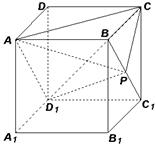
①三棱锥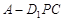 的体积不变;②
的体积不变;②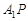 ∥平面
∥平面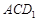 ;
;
③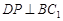 ;④平面
;④平面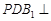 平面
平面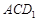 .
.
其中正确的命题序号是 .
①②④
解析试题分析:
对于①,容易证明AD1∥BC1,从而BC1∥平面AD1C,故BC1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,则三棱锥A-D1PC的体积不变;正确;对于②,连接A1B,A1C1容易证明A1C1∥AD1且相等,由于①知:AD1∥BC1,所以BA1C1∥面ACD1,从而由线面平行的定义可得;正确;对于③由于DC⊥平面BCB1C1,所以DC⊥BC1平面,若DP⊥BC1,则DC与DP重合,与条件矛盾;错误;对于④,连接DB1,容易证明DB1⊥面ACD1,从而由面面垂直的判定知:正确.故答案为:①②④
考点:直线与平面平行的判定直线与平面垂直的判定平面与平面垂直的判定.
点评:本题考查三棱锥体积求法中的等体积法;线面平行、垂直的判定,要注意使用转化的思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com