
【题目】定义在实数集上的可导函数![]() 是偶函数,若对任意实数
是偶函数,若对任意实数![]() 都有
都有![]() 恒成立,则使关于
恒成立,则使关于![]() 的不等式
的不等式![]() 成立的数
成立的数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.(-1,1)C.
B.(-1,1)C.![]() D.
D.![]()
【答案】C
【解析】
根据已知构造合适的函数,对函数求导,根据函数的单调性,求出函数的取值范围,并根据偶函数的性质的对称性,求出x<0的取值范围.
解:当x>0时,由![]() 可知:两边同乘以2x得:
可知:两边同乘以2x得:
2xf(x)+x2f′(x)﹣2x<0;
设:g(x)=x2f(x)﹣x2,
则g′(x)=2xf(x)+x2f′(x)﹣2x<0恒成立;
∴g(x)在(0,+∞)单调递减,
由x2f(x)﹣f(1)>x2﹣1;
∴x2f(x)﹣x2>f(1)﹣1;
即g(x)>g(1),
即0<x<1;
由于函数f(x)是偶函数,∴g(﹣x)=(﹣x)2f(﹣x)﹣(﹣x)2=x2f(x)﹣x2=g(x);
所以g(x)=x2f(x)﹣x2也是偶函数;
当x<0时,同理得:﹣1<x<0.
综上可知:实数x的取值范围为:(﹣1,0)∪(0,1).
故选:C.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中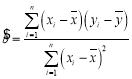
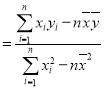 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{![]() }的前n项和为Sn,
}的前n项和为Sn,![]() ,且对任意的n∈N*,n≥2都有
,且对任意的n∈N*,n≥2都有![]() 。
。
(1)若![]() 0,
0,![]() ,求r的值;
,求r的值;
(2)数列{![]() }能否是等比数列?说明理由;
}能否是等比数列?说明理由;
(3)当r=1时,求证:数列{![]() }是等差数列。
}是等差数列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金(奖金额![]() 元)、专业二等奖学金(奖金额
元)、专业二等奖学金(奖金额![]() 元)及专业三等奖学金(奖金额
元)及专业三等奖学金(奖金额![]() 元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校
元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校![]() 年
年![]() 名学生周课外平均学习时间频率分布直方图,图(2)是这
名学生周课外平均学习时间频率分布直方图,图(2)是这![]() 名学生在
名学生在![]() 年周课外平均学习时间段获得专业奖学金的频率柱状图.
年周课外平均学习时间段获得专业奖学金的频率柱状图.
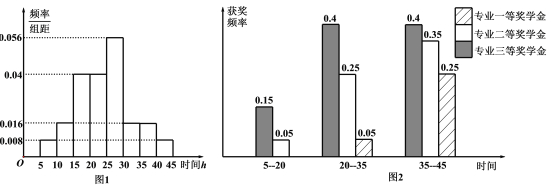
(Ⅰ)求这![]() 名学生中获得专业三等奖学金的人数;
名学生中获得专业三等奖学金的人数;
(Ⅱ)若周课外平均学习时间超过![]() 小时称为“努力型”学生,否则称为“非努力型”学生,列
小时称为“努力型”学生,否则称为“非努力型”学生,列![]() 联表并判断是否有
联表并判断是否有![]() 的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
(Ⅲ)若以频率作为概率,从该校任选一名学生,记该学生![]() 年获得的专业奖学金额为随机变量
年获得的专业奖学金额为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
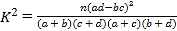
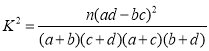
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com