
【题目】设![]() 是不同的直线,
是不同的直线, ![]() 是不同的平面,已知
是不同的平面,已知![]() ,下列说法正确的是 ( )
,下列说法正确的是 ( )
A. 若![]() ,则
,则![]() B. 若
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]() D. 若
D. 若![]() ,则
,则![]()
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() 、
、![]() ,并且经过点
,并且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() :
:![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() .当
.当![]() ,且满足
,且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中
万元,其中![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
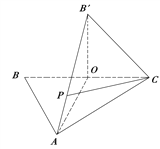
【题目】如图, ![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() .将
.将![]() 沿
沿
![]() 折起,使
折起,使![]() 点与图中
点与图中![]() 点重合.
点重合.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当三棱锥![]() 的体积取最大时,求二面角
的体积取最大时,求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(Ⅰ)设该厂每x天购买一次原材料,试写出每次购买的原材料在x天内总的保管费用y1关于x的函数关系式;
(Ⅱ)求该厂多少天购买一次原材料才能使平均每天支付的总费用y最少,并求出这个最少(小)值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com