
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 上的两点,线段
上的两点,线段![]() 的中点在直线
的中点在直线![]() 上.
上.
(1)当直线![]() 的斜率
的斜率![]() 存在时,求实数
存在时,求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是椭圆
是椭圆![]() 的左焦点,若椭圆
的左焦点,若椭圆![]() 上存在一点
上存在一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为椭圆
为椭圆![]() :
:![]() 的下顶点,椭圆长半轴的长等于椭圆的短轴长,且椭圆
的下顶点,椭圆长半轴的长等于椭圆的短轴长,且椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆的方程;
(2)过点![]() 的直线与直线
的直线与直线![]() 交于点
交于点![]() ,与椭圆交于
,与椭圆交于![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交直线
交直线![]() 交于点
交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国已进入新时代中国特色社会主义时期,人民生活水平不断提高,某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为![]() 元)的情况,并根据统计数据制成如下频率分布直方图.
元)的情况,并根据统计数据制成如下频率分布直方图.

(1)根据频率分布直方图估算![]() 的平均值
的平均值![]() ;
;
(2)视样本中的频率为概率,现从该市所有住户中随机抽取![]() 次,每次抽取
次,每次抽取![]() 户,每次抽取相互独立,设
户,每次抽取相互独立,设![]() 为抽出
为抽出![]() 户中
户中![]() 值不低于
值不低于![]() 元的户数,求
元的户数,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知抛物线C:y2=2px(p>0)的焦点为F,过F垂直于x轴的直线与C相交于A、B两点,△AOB的面积为2.
(1)求抛物线C的方程;
(2)若过P(![]() ,0)的直线与C相交于M,N两点,且
,0)的直线与C相交于M,N两点,且![]() 2
2![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左右焦点分别为F1、F2,过F1的直线交椭圆C与A、B两点,△AF2B的周长为
的左右焦点分别为F1、F2,过F1的直线交椭圆C与A、B两点,△AF2B的周长为![]() ,且椭圆C经过点
,且椭圆C经过点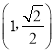 .
.
(1)求椭圆C的方程;
(2)当AB的中点坐标为![]() 时,求△AF2B的面积.
时,求△AF2B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com