练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)的定义域是R，f(0)＝2，对任意x∈R，f(x)＋f′(x)>1，则不等式ex·f(x)>ex＋1的解集为______．

     

    (0，＋∞)

    【解析】构造函数g(x)＝ex·f(x)－ex，因为g′(x)＝ex·f(x)＋ex·f′(x)－ex＝ex[f(x)＋f′(x)]－ex>ex－ex＝0，所以g(x)＝ex·f(x)－ex为R上的增函数．又因为g(0)＝e0·f(0)－e0＝1，所以原不等式转化为g(x)>g(0)，解得x>0.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测1练习卷（解析版） 题型：解答题

    已知函数f(x)＝ax＋x2，g(x)＝xln a，a>1.

    (1)求证：函数F(x)＝f(x)－g(x)在(0，＋∞)上单调递增；

    (2)若函数y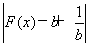＝－3有四个零点，求b的取值范围；

    (3)若对于任意的x1，x2∈[－1,1]时，都有|F(x2)－F(x1)|≤e2－2恒成立，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用8练习卷（解析版） 题型：填空题

    已知向量a＝(2，x)，b＝(x－1,1)，若a∥b，则x的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用6练习卷（解析版） 题型：填空题

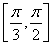    若函数f(x)＝sin ωx(ω>0)在区间上单调递增，在区间上单调递减，则ω＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用5练习卷（解析版） 题型：解答题

    已知x＝3是函数f(x)＝aln(1＋x)＋x2－10x的一个极值点．

    (1)求a；

    (2)求函数f(x)的单调区间；

    (3)若直线y＝b与函数y＝f(x)的图象有3个交点，求b的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用4练习卷（解析版） 题型：解答题

    设f(x)＝a(x－5)2＋6ln x，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线与y轴相交于点(0,6)．

    (1)确定a的值；

    (2)求函数f(x)的单调区间与极值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用4练习卷（解析版） 题型：填空题

    已知函数f(x)＝x3＋ax2＋x＋2(a>0)的极大值点和极小值点都在区间(－1,1)内，则实数a的取值范围是______．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用2练习卷（解析版） 题型：解答题

    设函数f(x)＝ax2＋bx＋b－1(a≠0)．

    (1)当a＝1，b＝－2时，求函数f(x)的零点；

    (2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用1练习卷（解析版） 题型：解答题

    已知二次函数f(x)＝ax2＋bx＋1(a＞0)，F(x)＝若f(－1)＝0，且对任意实数x均有f(x)≥0成立．

    (1)求F(x)的表达式；

    (2)当x∈[－2,2]时，g(x)＝f(x)－kx是单调函数，求k的取值范围．

     

    查看答案和解析>>

    同步练习册答案