
【题目】数列{an}的通项公式an=ncos ![]() ,其前n项和为Sn , 则S2015=( )
,其前n项和为Sn , 则S2015=( )
A.1008
B.2015
C.﹣1008
D.﹣504
【答案】C
【解析】解:∵an=ncos ![]() , 又∵f(n)=cos
, 又∵f(n)=cos ![]() 是以T=4为周期的周期函数,
是以T=4为周期的周期函数,
∴a1+a2+a3+a4=(0﹣2+0+4)=2,a5+a6+a7+a8=(0﹣6+0+8)=2,
…
a2009+a2010+a2011+a2012=(0﹣2010+0+2012)=2,
a2013+a2014+a2015=﹣2014.
S2015=a1+a2+a3+a4+…+a2015
=(0﹣2+0+4)+(0﹣6+0+8)+…+(0﹣2010+0+2012)﹣2014
=2×503﹣2014=1006﹣2014=﹣1008.
故选:C.
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系 才能得出正确答案.
才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组抽出的号码为28,则第8组抽出的号码应是a;若用分层抽样方法,则50岁以下年龄段应抽取b人,那么a+b等于( ) 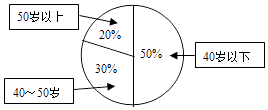
A.46
B.45
C.70
D.69
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}前n项和为Sn , 且满足a2=2,S5=15;等比数列{bn}满足b2=4,b5=32.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=λan+2n(n∈N* , λ∈R),且a1=2.
(1)若λ=1,求数列{an}的通项公式;
(2)若λ=2,证明数列{ ![]() }是等差数列,并求数列{an}的前n项和Sn .
}是等差数列,并求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:ax﹣y+a=0,l2:x+ay﹣a(a+1)=0,l3:(a+1)x﹣y+a+1=0,a>0.
(1)证明:这三条直线共有三个不同的交点;
(2)求这三条直线围成的三角形的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x﹣y|=2”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过不重合的A(m2+2,m2﹣3),B(3﹣m﹣m2 , 2m)两点的直线l倾斜角为45°,则m的取值为( )
A.m=﹣1
B.m=﹣2
C.m=﹣1或2
D.m=l或m=﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn表示数列{an}的前n项的和,且 ![]()
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com