
【题目】设命题![]() 对任意
对任意![]() ,不等式
,不等式![]() 恒成立;命题q:存在
恒成立;命题q:存在![]() ,使得不等式
,使得不等式![]() 成立.
成立.
(1)若p为真命题,求实数m的取值范围;
(2)若命题p、q有且只有一个是真命题,求实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
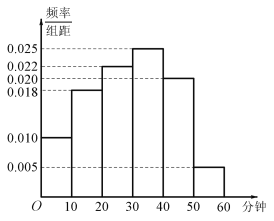
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的2×2列联表;
(2)根据此资料,判断是否有![]() 的把握认为“体育迷”与性别有关?
的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附: ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.


(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为ξ,求ξ的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有形状、大小都相同的5张卡片,其中有2张卡片写着文字“中”,2张卡片写着文字“国”,1张卡片写着文字“梦”.若从中任意取出3张,则取出的3张卡片上的文字能组成“中国梦”的概率为____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形, ![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长
的长![]() ,若不存在,请说明理由.
,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为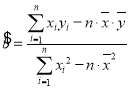 ;
;![]()
本题参考数值:![]() .
.
(1)若销量y与单价x服从线性相关关系,求该回归方程;
(2)在(1)的前提下,若该产品的成本是5元/件,问:产品该如何确定单价,可使工厂获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了增强民众防控病毒的意识,举行了“预防新冠病毒知识竞赛”网上答题,随机抽取![]() 人,答题成绩统计如图所示.
人,答题成绩统计如图所示.
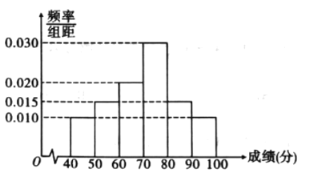
(1)由直方图可认为答题者的成绩![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() 分别为答题者的平均成绩
分别为答题者的平均成绩![]() 和成绩的方差
和成绩的方差![]() ,那么这
,那么这![]() 名答题者成绩超过
名答题者成绩超过![]() 分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
(2)如果成绩超过![]() 分的民众我们认为是“防御知识合格者”,用这
分的民众我们认为是“防御知识合格者”,用这![]() 名答题者的成绩来估计全市的民众,现从全市中随机抽取
名答题者的成绩来估计全市的民众,现从全市中随机抽取![]() 人,“防御知识合格者”的人数为
人,“防御知识合格者”的人数为![]() ,求
,求![]() .(精确到
.(精确到![]() )
)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某品牌饮料的某种食品添加剂是否超标,现对该品牌下的两种饮料一种是碳酸饮料![]() 含二氧化碳
含二氧化碳![]() ,另一种是果汁饮料
,另一种是果汁饮料![]() 不含二氧化碳
不含二氧化碳![]() 进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶
进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶![]() 均是
均是![]() 组成的一个样本,进行了检测,得到了如下茎叶图
组成的一个样本,进行了检测,得到了如下茎叶图![]() 根据国家食品安全规定当该种添加剂的指标大于
根据国家食品安全规定当该种添加剂的指标大于![]() 毫克
毫克![]() 为偏高,反之即为正常.
为偏高,反之即为正常.
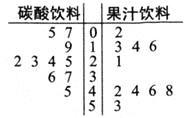
(1)依据上述样本数据,完成下列![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
正常 | 偏高 | 合计 | |
碳酸饮料 | |||
果汁饮料 | |||
合计 |
(2)现从食品添加剂偏高的样本中随机抽取2瓶饮料去做其它检测,求这两种饮料都被抽到的概率.
参考公式: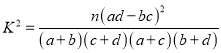 ,其中
,其中![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com