
(本小题13分)
在正方体ABCD—A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.
求证:(Ⅰ)MN//平面ABCD;(Ⅱ)MN⊥平面B1BG.
科目:高中数学 来源: 题型:
 (本小题13分)已知函数
(本小题13分)已知函数![]()
(1)用五点法画出它在一个周期
内的闭区间上的图象;
(2)指出![]() 的周期、
的周期、
振幅、初相、对称轴;
(3)说明此函数图象可由
![]() 上的图象经
上的图象经
怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省德州市高三12月月考理科数学试卷(解析版) 题型:解答题
(本小题13分)在平面直角坐标系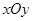 中,
中, 是抛物线
是抛物线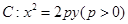 的焦点,
的焦点,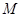 是抛物线
是抛物线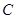 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过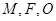 三点的圆的圆心为
三点的圆的圆心为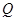 ,点
,点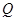 到抛物线
到抛物线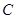 的准线的距离为
的准线的距离为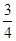 .
.
(Ⅰ)求抛物线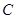 的方程;
的方程;
(Ⅱ)是否存在点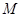 ,使得直线
,使得直线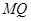 与抛物线
与抛物线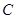 相切于点
相切于点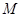 ?若存在,求出点
?若存在,求出点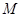 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期第一次月考数学试卷(解析版) 题型:解答题
(本小题13分)已知函数f(x)=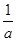 -
-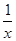 (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[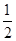 ,2]上的值域是[
,2]上的值域是[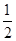 ,2],求a的值.
,2],求a的值.
查看答案和解析>>
科目:高中数学 来源:2014届江西省上饶市高一下学期第一次月考数学 题型:解答题
(本小题13分)在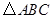 中,内角
中,内角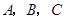 对边的边长分别是
对边的边长分别是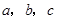 ,已知
,已知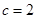 ,
,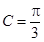 .
.
(Ⅰ)若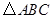 的面积等于
的面积等于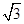 ,求
,求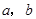 ;
;
(Ⅱ)若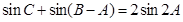 ,求
,求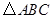 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com