
【题目】某个比赛安排4名志愿者完成6项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式有多少种( )
A.7200种B.4800种C.2640种D.1560种
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高一某班的元旦文艺晚会中,有这么一个游戏:一盒子内装有6张大小和形状完全相同的卡片,每张卡片上写有一个成语,它们分别为意气风发、风平浪静、心猿意马、信马由缰、气壮山河、信口开河,从盒内随机抽取2张卡片,若这2张卡片上的2个成语有相同的字就中奖,则该游戏的中奖率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求实数a的值;
(2)判断该函数在定义域R上的单调性(不要求写证明过程).
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(4)设关于x的函数![]() 有零点,求实数b的取值范围.
有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至10月24日,中国共产党第十九次全国代表大会![]() 简称党的“十九大”
简称党的“十九大”![]() 在北京召开
在北京召开![]() 一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在
一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在![]() 内,按成绩分成5组:第1组
内,按成绩分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
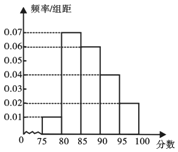
![]() 求这100人的平均得分
求这100人的平均得分![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 求第3,4,5组分别选取的作深入学习的人数;
求第3,4,5组分别选取的作深入学习的人数;
![]() 若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 满足以下4个条件.
满足以下4个条件.
①函数![]() 的定义域是
的定义域是![]() ,且其图象是一条连续不断的曲线;
,且其图象是一条连续不断的曲线;
②函数![]() 在
在![]() 不是单调函数;
不是单调函数;
③函数![]() 是偶函数;
是偶函数;
④函数![]() 恰有2个零点.
恰有2个零点.
(1)写出函数![]() 的一个解析式;
的一个解析式;
(2)画出所写函数![]() 的解析式的简图;
的解析式的简图;
(3)证明![]() 满足结论③及④.
满足结论③及④.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机生产企业为了解消费者对某款手机的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有20份给予回复,这20份的评分如下:
男 | 47,36,28,48,48,44,50,46,50,37,35,49 |
女 | 38,37,50,36,38,45,29,39 |
(1)完成下面的茎叶图,并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值;
男 | 女 | |
2 | ||
3 | ||
4 | ||
5 |
满意 | 不满意 | 合计 | |
男 | |||
女 | |||
合计 |
(2)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
(3)若从回复的20名消费者中按性别用分层抽样的方法抽取5人,再从这5人中随机抽取2人作进一步调查,求至少有1名女性消费者被抽到的概率.
附:
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com