
【题目】综合题
(1)已知函数f(x)=2x+ ![]() (x>0),证明函数f(x)在(0,
(x>0),证明函数f(x)在(0, ![]() )上单调递减,并写出函数f(x)的单调递增区间;
)上单调递减,并写出函数f(x)的单调递增区间;
(2)记函数g(x)=a|x|+2ax(a>1) ①若a=4,解关于x的方程g(x)=3;
②若x∈[﹣1,+∞),求函数g(x)的值域.
【答案】
(1)证明:设x1,x2是区间(0, ![]() )上的任意两个实数,且x1<x2,
)上的任意两个实数,且x1<x2,
则f(x1)﹣f(x2)=2(x1﹣x2)+( ![]() ﹣
﹣ ![]() )=
)= ![]() ,
,
因为0<x1<x2< ![]() ,所以x1﹣x2<0,0<x1x2<
,所以x1﹣x2<0,0<x1x2< ![]() ,故2x1x2﹣1<0,
,故2x1x2﹣1<0,
所以f(x1)﹣f(x2)>0,即f(x1)>f(x2),
所以函数f(x)在(0, ![]() )上单调递减,
)上单调递减,
函数f(x)的单调递增区间为( ![]() ,+∞).
,+∞).
(2)解:①当a=4时,4|x|+24x=3,
(ⅰ)当x≥0时,4x+24x=3,即4x=1,所以x=0;
(ⅱ)当x<0时,4﹣x+24x=3,
即2(4x)2﹣34x+1=0,
解得:4x=1或4x= ![]() ,
,
所以x=﹣ ![]() 或0(舍去);
或0(舍去);
综上所述,方程g(x)=3的解为x=0或x=﹣ ![]() ;
;
②(ⅰ)当x≥0时,g(x)=3ax,其中a>1,
所以g(x)在[0,+∞)上单调递增,g(x)min=g(0)=3,
所以g(x)在[0,+∞)上的值域为[3,+∞);
(ⅱ)当x∈[﹣1,0)时,g(x)=a﹣x+2ax,其中a>1,
令t=ax,则t∈[ ![]() ,1),g(x)=2t+
,1),g(x)=2t+ ![]() =f(t),
=f(t),
(ⅰ)若1<a≤ ![]() ,则
,则 ![]() ≥
≥ ![]() ,
,
据(1)可知,f(t)=2t+ ![]() 在[
在[ ![]() ,1)上单调递增,
,1)上单调递增,
所以f( ![]() )≤f(t)<f(1),且f(
)≤f(t)<f(1),且f( ![]() )=a+
)=a+ ![]() ,f(1)=3,
,f(1)=3,
此时,g(x)在[﹣1,0)上的值域为[a+ ![]() ,3);
,3);
(ⅱ)若a> ![]() ,则
,则 ![]() <
< ![]() ,
,
据(1)可知,f(t)=2t+ ![]() 在[
在[ ![]() ,
, ![]() )上单调递减,在(
)上单调递减,在( ![]() ,1)上单调递增,
,1)上单调递增,
所以f(t)min=f( ![]() )=2
)=2 ![]() ,又f(
,又f( ![]() )=a+
)=a+ ![]() ,f(1)=3,
,f(1)=3,
当f( ![]() )≥f(1)时,g(x)在[﹣1,0)上的值域为[2
)≥f(1)时,g(x)在[﹣1,0)上的值域为[2 ![]() ,a+
,a+ ![]() ],
],
当f( ![]() )<f(1)时,g(x)在[﹣1,0)上的值域为[2
)<f(1)时,g(x)在[﹣1,0)上的值域为[2 ![]() ,3);
,3);
综上所述,当1<a≤ ![]() 时,函数g(x)在[﹣1,+∞)上的值域为[a+
时,函数g(x)在[﹣1,+∞)上的值域为[a+ ![]() ,+∞;
,+∞;
当a> ![]() 时,函数g(x)在[﹣1,+∞)上的值域为[2
时,函数g(x)在[﹣1,+∞)上的值域为[2 ![]() ,+∞).
,+∞).
【解析】(1)根据函数单调性的定义证明即可;(2)①将a=4带入g(x),通过讨论x的正负,去掉绝对值号,解方程即可;②通过讨论x的范围,求出g(x)的单调性,从而求出g(x)的值域即可.
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,以及对函数的单调性的理解,了解注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.


科目:高中数学 来源: 题型:
【题目】已知:θ为第一象限角, ![]() =(sin(θ﹣π),1),
=(sin(θ﹣π),1), ![]() =(sin(
=(sin( ![]() ﹣θ),﹣
﹣θ),﹣ ![]() ),
),
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)若| ![]() +
+ ![]() |=1,求sinθ+cosθ的值.
|=1,求sinθ+cosθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|f(x)=lg(x﹣1)+ ![]() },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ![]() ,求A∪B;
,求A∪B;
(2)若A∩B=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,经过村庄A有两条互相垂直的笔直公路AB和AC,根据规划拟在两条公路围成的直角区域内建一工厂P,为了仓库存储和运输方便,在两条公路上分别建两个仓库M,N(异于村庄A,将工厂P及仓库M,N近似看成点,且M,N分别在射线AB,AC上),要求MN=2,PN=1(单位:km),PN⊥MN. 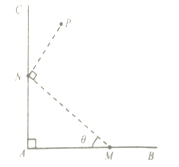
(1)设∠AMN=θ,将工厂与村庄的距离PA表示为θ的函数,记为l(θ),并写出函数l(θ)的定义域;
(2)当θ为何值时,l(θ)有最大值?并求出该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知t为实数,函数f(x)=2loga(2x+t﹣2),g(x)=logax,其中0<a<1.
(1)若函数y=g(ax+1)﹣kx是偶函数,求实数k的值;
(2)当x∈[1,4]时,f(x)的图象始终在g(x)的图象的下方,求t的取值范围;
(3)设t=4,当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],若n﹣m的最小值为 ![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:点M(1,3)不在圆(x+m)2+(y﹣m)2=16的内部,命题q:“曲线 ![]() 表示焦点在x轴上的椭圆”,命题s:“曲线
表示焦点在x轴上的椭圆”,命题s:“曲线 ![]() 表示双曲线”.
表示双曲线”.
(1)若“p且q”是真命题,求m的取值范围;
(2)若q是s的必要不充分条件,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com