
【题目】已知函数![]() ,若曲线
,若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求![]() 的值;
的值;
(2)函数![]() 恰有两个零点
恰有两个零点![]() ,求函数
,求函数![]() 的单调区间及实数
的单调区间及实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)依题意可知,切线的斜率为![]() ,即
,即![]() ,由此解得
,由此解得![]() ;(2)先求得
;(2)先求得![]() 的表达式,
的表达式,![]() ,利用导数可求得
,利用导数可求得![]() 的极小值,也即是最小值,只需最小值小于零就可以.由此求得取值范围是
的极小值,也即是最小值,只需最小值小于零就可以.由此求得取值范围是![]() .
.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() .由
.由![]() ,且
,且![]() ,解得a=1.
,解得a=1.
(2)因为![]()
![]() 则
则![]() .
.
(ⅰ)当![]() 即
即![]() 时,
时,![]() ,所以g(x)在
,所以g(x)在![]() 上单调递减此时只存在一个零点,不合题意.
上单调递减此时只存在一个零点,不合题意.
(ⅱ)当m<1时,令![]() ,解得
,解得![]() .
.
当x变化时,g(x)与![]() 的变化情况如下表:
的变化情况如下表:
x | (0, |
|
|
| — | 0 | + |
g(x) | ↘ | 极小值 | ↗ |
由题意可知,![]() .
.
下面判断极小值的正负。
设![]() ,m<1
,m<1
(1)当m=0时,h(0)=0,即![]()
此时g(x)恰有一个零点不合题意。
(2)当![]() 时,
时,![]()
当m<0时,![]() ; 当0<m<1时,
; 当0<m<1时,![]()
所以h(m)在![]() 上单调递增,在(0,1)单调递减。
上单调递增,在(0,1)单调递减。
所以h(m)<h(0)=0,此时g(x)恰有两个零点。
综上,m的取值范围是![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇.2016年“618”期间,某购物平台的销售业绩高达516亿元人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)选完成关于商品和服务评价的![]() 列联表,再判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
列联表,再判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量![]() :
:
①求对商品和服务全为好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: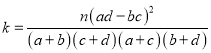 (其中
(其中![]() )关于商品和服务评价的
)关于商品和服务评价的![]() 列联表:
列联表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 80 | ||
对商品不满意 | 10 | ||
合计 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从孝感地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A. 简单的随机抽样 B. 按性别分层抽样 C. 按学段分层抽样 D. 系统抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度![]() (单位:千米时)是车流密度
(单位:千米时)是车流密度![]() (单位:辆千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/时.研究表明:当
(单位:辆千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/时.研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时![]() )可以达到最大,并求出最大值.(精确到1辆/时)
)可以达到最大,并求出最大值.(精确到1辆/时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求函数
处有极值,求函数![]() 的最大值;
的最大值;
(2)①是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A. 三点确定一个平面 B. 依次首尾相接的四条线段必共面
C. 直线与直线外一点确定一个平面 D. 两条直线确定一个平面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com