
【题目】设直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() 。
。
(1)写出直线![]() 的标准参数方程;
的标准参数方程;
(2)设此直线与曲线![]()
![]() (
( ![]() 为参数)交于
为参数)交于![]() 两点,求
两点,求![]() 的值。
的值。
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 点,动圆
点,动圆![]() 与直线
与直线![]() 相切,并且与圆
相切,并且与圆![]() 相外切,
相外切,
(1)求动圆的圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若过原点且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,问是否存在以
两点,问是否存在以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,直线
,直线![]() 与抛物线C交于A,B两点.
与抛物线C交于A,B两点.
(1)若直线![]() 过抛物线C的焦点,求
过抛物线C的焦点,求![]() .
.
(2)已知抛物线C上存在关于直线![]() 对称的相异两点M和N,求
对称的相异两点M和N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥C的底面是正方形,PA⊥平面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PEC
(2)求证:平面PCD⊥平面PEC;
(3)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1,
=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1, ![]() ).过椭圆E内一点P(1,
).过椭圆E内一点P(1, ![]() )的两条直线分别与椭圆交于点A、C和B、D,且满足
)的两条直线分别与椭圆交于点A、C和B、D,且满足 ![]() ,其中λ为实数.当直线AP平行于x轴时,对应的λ=
,其中λ为实数.当直线AP平行于x轴时,对应的λ= ![]() .
. 
(1)求椭圆E的方程;
(2)当λ变化时,kAB是否为定值?若是,请求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
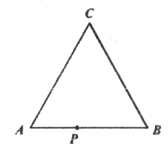
【题目】如图,某机器人的运动轨道是边长为1米的正三角形ABC,开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变一次运动方向(假设按此方式无限运动下去),运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2,x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2,机器人到A点的距离d与x满足函数关系d=f(x),现有如下结论:
①f(x)的值域为[0,1];
②f(x)是以3为周期的函数;
③f(x)是定义在R上的奇函数;
④f(x)在区间[-3,-2]上单调递增.
其中正确的有_________(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若f(1)=2,求函数y=f(x)-2x在[![]() ,2]上的值域;
,2]上的值域;
(Ⅱ)当a∈(0,![]() )时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
)时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com