
 …
…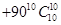 除以88的余数是( )
除以88的余数是( )| A.-1 | B.-87 | C.1 | D.87 |
科目:高中数学 来源:不详 题型:单选题
| A.96种 | B.180种 | C.240种 | D.280种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
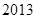 年第
年第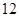 届全国运动会将在沈阳举行,某校
届全国运动会将在沈阳举行,某校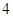 名大学生申请当
名大学生申请当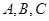 三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务
三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务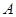 比赛项目,则不同的安排方案共有
比赛项目,则不同的安排方案共有A.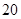 种 种 | B.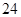 种 种 | C.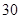 种 种 | D.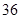 种 种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com