
【题目】(2016年苏州B19)已知函数f(x)=x|x-a|,a∈R,g(x)=x2-1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.
【答案】(1)![]() (2)
(2)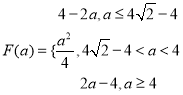
【解析】
【试题分析】(1)借助绝对值的定义讨论当x≥1和x<1两种情形下两个不等式的解集,最后求这两个二次不等式的并集;(2)依据题设条件运用分类整合思想,对实数a≤0;0<a<2;a≥2分三种情形,分别求出函数f(x)在区间[0,2]上的解析式,进而求出其最大值F(a),然后再运用分段函数表示函数F(a)的解析式:
(1)解:f(x)≥g(x),a=1时,即解不等式x|x-1|≥x2-1,
当x≥1时,不等式为x2-x≥x2-1,解得x≤1,所以x=1;
当x<1时,不等式为x-x2≥x2-1,解得![]() ,
,
所以![]() ; 综上, x∈
; 综上, x∈![]() .
.
(2)因为x∈[0,2],当a≤0时,f(x)=x2-ax,则f(x)在区间[0,2]上是增函数,
所以F(a)=f(2)=4-2a;
当0<a<2时, ,则f(x)在区间
,则f(x)在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,在区间[a,2]上是增函数,所以F(a)=max{f(
上是减函数,在区间[a,2]上是增函数,所以F(a)=max{f(![]() ),f(2)},
),f(2)},
而![]() ,f(2)=4-2a,令
,f(2)=4-2a,令![]() 即
即![]() ,
,
解得![]() ,
,
所以当![]() 时,F(a)= 4-2a;
时,F(a)= 4-2a;
令![]() 即
即![]() ,解得
,解得![]() 或
或![]() ,
,
所以当![]() 时,
时,![]() ;
;
当a≥2时,f(x)=-x2+ax,
当![]() 即2≤a<4时,f(x)在间
即2≤a<4时,f(x)在间![]() 上是增函数,在
上是增函数,在![]() 上是减函数,则
上是减函数,则![]() ;
;
当![]() ,即a≥4时,f(x)在间[0,2]上是增函数,则
,即a≥4时,f(x)在间[0,2]上是增函数,则![]() ;
;
所以,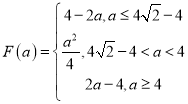 ,
,


科目:高中数学 来源: 题型:
【题目】一古寺有一池储满了水,现一小和尚每日,按照池中所剩水一定的百分率打走一些水,且每次打水的百分率一样.10日过去,池中水恰为满池水的一半.
(1)求此百分率.(保留指数形式)
(2)若某日小和尚打完水,池中水为满池水的![]() 倍,小和尚已打水几日?
倍,小和尚已打水几日?
(3)若某日小和尚打完水,池中水为满池水的![]() 倍,若古寺要求池中水不少于满池水的
倍,若古寺要求池中水不少于满池水的![]() ,则小和尚还能再打几日水?
,则小和尚还能再打几日水?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面![]() 内有不共线的三点到平面
内有不共线的三点到平面![]() 的距离相等,则
的距离相等,则![]() ;④过平面
;④过平面![]() 的一条斜线,有且只有一个平面与平面
的一条斜线,有且只有一个平面与平面![]() 垂直.其中正确的是( )
垂直.其中正确的是( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车收费标准如下:起步价为8元,起步里程为3km(不超过3km按起步价付费);超过3km但不超过8km时,超过部分按每千米2.15元收费:超过8km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是( )
A.出租车行驶2km,乘客需付费8元
B.出租车行驶4km,乘客需付费9.6元
C.出租车行驶10km,乘客需付费25.45元
D.某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用
E.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9km
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() .
.
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
(3)若f(x)为奇函数,求满足f(ax)<f(2)的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司有750辆电动汽车供租赁使用,管理这些电动汽车的费用是每日![]() 元.根据调查发现,若每辆电动汽车的日租金不超过90元,则电动汽车可以全部租出;若超过90元,则每超过1元,租不出去的电动汽车就增加3辆.设每辆电动汽车的日租金为
元.根据调查发现,若每辆电动汽车的日租金不超过90元,则电动汽车可以全部租出;若超过90元,则每超过1元,租不出去的电动汽车就增加3辆.设每辆电动汽车的日租金为![]() 元(
元(![]() ),用
),用![]() (单位:元)表示出租电动汽车的日净收入.(日净收入等于日出租电动汽车的总收入减去日管理费用)
(单位:元)表示出租电动汽车的日净收入.(日净收入等于日出租电动汽车的总收入减去日管理费用)
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)试问当每辆电动汽车的日租金为多少元时?才能使日净收入最多,并求出日净收入的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月对甲、乙两种移动支付方式的使用情况,从全校学生中随机抽取了100人作为样本,发现样本中甲、乙两种支付方式都不使用的有10人,样本中仅使用甲种支付方式和仅使用乙种支付方式的学生的支付金额分布情况如下:
支付金额(元) 支付方式 |
|
| 大于1000 |
仅使用甲 | 15人 | 8人 | 2人 |
仅使用乙 | 10人 | 9人 | 1人 |
(1)从全校学生中随机抽取1人,估计该学生上个月甲、乙两种支付方式都使用的概率;
(2)从样本中仅使用甲种支付方式和仅使用乙种支付方式的学生中各随机抽取1人,以![]() 表示这2人中上个月支付金额大于500元的人数,用频率近似代替概率,求
表示这2人中上个月支付金额大于500元的人数,用频率近似代替概率,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com