
【题目】某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部
竞选.
(Ⅰ)设所选3人中女生人数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率.
科目:高中数学 来源: 题型:
【题目】某地为了了解地区100000户家庭的用电情况,采用分层抽样的方法抽取了500户家庭的月均用电量,并根据这500户家庭的月均用电量画出频率分布直方图(如图),则该地区100000户家庭中月均用电度数在[70,80]的家庭大约有户. 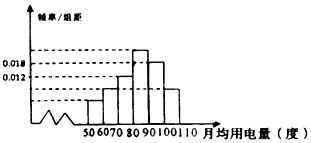
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣a|x﹣1|+b(a>0,b>﹣1)
(1)若b=0,a>2,求f(x)在区间[0,2]内的最小值m(a);
(2)若f(x)在区间[0,2]内不同的零点恰有两个,且落在区间[0,1),(1,2]内各一个,求a﹣b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣lnx(a∈R)
(1)当a=1时,求函数y=f(x)的单调区间;
(2)若x∈(0,1],|f(x)|≥1恒成立,求a的取值范围;
(3)若a= ![]() ,证明:ex﹣1f(x)≥x.
,证明:ex﹣1f(x)≥x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 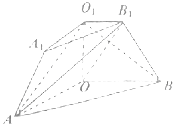
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣lnx(a∈R)
(1)当a=1时,求函数y=f(x)的单调区间;
(2)若x∈(0,1],|f(x)|≥1恒成立,求a的取值范围;
(3)若a= ![]() ,证明:ex﹣1f(x)≥x.
,证明:ex﹣1f(x)≥x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(1)求证AM∥平面BDE;
(2)求二面角A﹣DF﹣B的大小;
(3)试在线段AC上一点P,使得PF与CD所成的角是60°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com