
【题目】已知曲线![]() 的方程为
的方程为![]() .
.
(1)当![]() 时,试确定曲线
时,试确定曲线![]() 的形状及其焦点坐标;
的形状及其焦点坐标;
(2)若直线![]() 交曲线
交曲线![]() 于点
于点![]() 、
、![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,试问此时曲线
,试问此时曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?
对称?
(3)当![]() 为大于1的常数时,设
为大于1的常数时,设![]() 是曲线
是曲线![]() 上的一点,过点
上的一点,过点![]() 作一条斜率为
作一条斜率为![]() 的直线
的直线![]() ,又设
,又设![]() 为原点到直线
为原点到直线![]() 的距离,
的距离,![]() 分别为点
分别为点![]() 与曲线
与曲线![]() 两焦点的距离,求证
两焦点的距离,求证![]() 是一个定值,并求出该定值.
是一个定值,并求出该定值.
【答案】(1) 曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,焦点坐标为
轴上的椭圆,焦点坐标为![]() ; (2) 见解析;(3)见证明
; (2) 见解析;(3)见证明
【解析】
(1)将a代入,两边平方并化简,可得曲线C的方程及形状;
(2)将![]() 代入曲线,利用PQ中点的横坐标为
代入曲线,利用PQ中点的横坐标为![]() ,求出m,验证判别式是否成立,可得结论.
,求出m,验证判别式是否成立,可得结论.
(3)将曲线C化简,得到焦点坐标,求得![]() ,再求得点到直线
,再求得点到直线![]() 的距离,代入
的距离,代入![]() 化简得到定值.
化简得到定值.
(1)当![]() 时,
时,![]() ,两边平方并化简得
,两边平方并化简得![]() ,
,
∴曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,其长半轴长为1,短半轴长为
轴上的椭圆,其长半轴长为1,短半轴长为![]() ,焦点坐标为
,焦点坐标为![]() ;
;
(2)将![]() 代入
代入![]() ,消去
,消去![]() ,
,
得![]() ,由题意,
,由题意,![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),此时,
(舍),此时,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,则
,则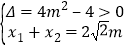 ,
,
![]() 的中点坐标为
的中点坐标为![]() 在对称轴
在对称轴![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
,
不满足![]() ,∴曲线
,∴曲线![]() 上不存在不同的两点
上不存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称;
对称;
(3)![]() ,两焦点坐标为
,两焦点坐标为![]() 、
、![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴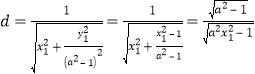 ,
,
用![]() 替换
替换![]() 中的
中的![]() ,
,
可得![]() ,∴
,∴![]() ,
,
∴![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】有下列四个命题:
(1)“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;
互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若![]() ,则
,则![]() 无实数解”的否命题;
无实数解”的否命题;
(4)命题:“空间中到一个正四面体的六条棱所在的直线距离均相等的点有且只有![]() 个”; 其中真命题( )
个”; 其中真命题( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:
①一支田径队有男女运动员98人,其中男运动员有56人.按男、女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是12人;
②在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8.
③废品率x%和每吨生铁成本y(元)之间的回归直线方程为![]() 2x+256,这表明废品率每增加1%,生铁成本大约增加258元;
2x+256,这表明废品率每增加1%,生铁成本大约增加258元;
④为了检验某种血清预防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防作用”,利用2×2列联表计算得K2的观测值k≈3.918,经查对临界值表知P(K2≥3841)≈0.05,由此,得出以下判断:在犯错误的概率不超过0.05的前提下认为“这种血清能起到预防的作用”,
正确的有( )
A.①②④B.①②③C.①③D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产某种产品,一条流水线年产量为![]() 件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
第一段生产的半成品质量指标 |
|
|
|
第二段生产的成品为一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生产的成品为二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生产的成品为三等品概率 | 0.5 | 0.3 | 0.1 |
从第一道生产工序抽样调查了![]() 件,得到频率分布直方图如图:
件,得到频率分布直方图如图:

若生产一件一等品、二等品、三等品的利润分别是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各组的中间值估计为该组半成品的质量指标,估算流水线第一段生产的半成品质量指标的平均值;
(Ⅱ)将频率估计为概率,试估算一条流水线一年能为该公司创造的利润;
(Ⅲ)现在市面上有一种设备可以安装到流水线第一段,价格是![]() 万元,使用寿命是
万元,使用寿命是![]() 年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布
年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布![]() ,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是![]() 年
年![]() 个重点城市(序号
个重点城市(序号![]() 为一线城市,其它为非一线城市)的月平均收入与房价对照表,根据表中数据并适当修正,得到房价中位数与月平均收入的线性回归方程是
为一线城市,其它为非一线城市)的月平均收入与房价对照表,根据表中数据并适当修正,得到房价中位数与月平均收入的线性回归方程是![]() ,我们把根据房价与月平均收入的线性回归方程得到的房价称为参考房价,若实际房价中位数大于参考房价,我们称这个城市是“房价偏贵城市”.
,我们把根据房价与月平均收入的线性回归方程得到的房价称为参考房价,若实际房价中位数大于参考房价,我们称这个城市是“房价偏贵城市”.
序号 | 月评价收入 | 房价中位数 | 参考房价 | 序号 | 月评价收入 | 房价中位数 | 参考房价 | 序号 | 月评价收入 | 房价中位数 | 参考房价 |
1 | 10670 | 67822 | 11 | 7081 | 17327 | 25704 | 21 | 7081 | 14792 | 15972 | |
2 | 10015 | 52584 | 51180 | 12 | 7065 | 13918 | 19476 | 22 | 7065 | 18741 | 15780 |
3 | 9561 | 50900 | 45732 | 13 | 7027 | 16286 | 19404 | 23 | 7027 | 10538 | 15324 |
4 | 8798 | 30729 | 36576 | 14 | 6974 | 16667 | 18204 | 24 | 6974 | 12069 | 14688 |
5 | 7424 | 10926 | 20088 | 15 | 6920 | 9743 | 17760 | 25 | 6920 | 2333 | 14040 |
6 | 7825 | 26714 | 24900 | 16 | 6903 | 10627 | 18120 | 26 | 6903 | 13582 | 13836 |
7 | 7770 | 39723 | 24240 | 17 | 6884 | 29000 | 17388 | 27 | 6884 | 22126 | 13608 |
8 | 7750 | 15114 | 24000 | 18 | 6654 | 7979 | 16584 | 28 | 6654 | 12207 | 10848 |
9 | 7723 | 17727 | 23676 | 19 | 6648 | 12500 | 16920 | 29 | 6648 | 12472 | 10776 |
10 | 7635 | 13012 | 22620 | 20 | 6608 | 12298 | 16200 | 30 | 6608 | 16406 | 10286 |
(1)计算城市![]() 的参考房价;
的参考房价;
(2)从![]() 个一线城市中随机选取
个一线城市中随机选取![]() 个城市进行调研,求恰好选到一个“房价偏贵城市”的概率;
个城市进行调研,求恰好选到一个“房价偏贵城市”的概率;
(3)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为一线城市与该城市为“房价偏贵城市”有关?
的把握认为一线城市与该城市为“房价偏贵城市”有关?
一般城市 | 非一线城市 | 总计 | |
房价偏贵城市 | |||
不是房价偏贵城市 | |||
总计 |
附参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
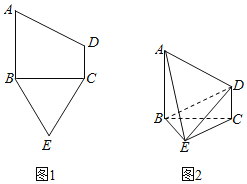
【题目】已知五边形ABECD有一个直角梯形ABCD与一个等边三角形BCE构成,如图1所示,![]() ,且
,且![]() ,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且
,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且![]() 平面BEC.
平面BEC.
![]() 求证:平面
求证:平面![]() 平面ADE;
平面ADE;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,动点M在边DC上(不同于D点),P为边AB上任意一点,沿AM将△ADM翻折成△AD'M,当平面AD'M垂直于平面ABC时,线段PD'长度的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com