Question

【题目】如图，在三棱锥V-ABC中，平面VAB平面ABC， VAB为等边三角形，ACBC且AC=BC=，O,M分别为AB,VA的中点。

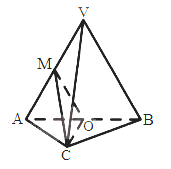
（I）求证：VB//平面MOC；

（II）求证：平面MOC平面VAB；

（III）求三棱锥V-ABC的体积。

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）见解析；（III）.

【解析】试题分析：（1）由中位线定理得OM//VB，故而VB∥平面MOC；

（2）由等腰三角形三线合一可知OC⊥AB，利用面面垂直的性质得出OC⊥平面VAB，进而证得平面MOC平面VAB；

（3）由勾股定理求出AB，OC，得出△VAB的面积，代入棱锥的体积公式即可．

试题解析：

（I）因为O,M分别为AB,VA的中点，

所以OM//VB

又因为VB平面MOC

所以VB//平面MOC

（II）因为AC=BC,O为AB的中点，

所以OCAB

又因为平面VAB平面ABC，且OC平面ABC，

所以OC平面VAB。

∴平面MOC平面VAB；

（III）在等腰直角三角形ACB中，AC=BC=，

所以AB=2，OC=1.

所以等边三角形VAB的面积.

又因为CO平面VAB,

所以三棱锥C-VAB的体积等于.

又因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等，

所以三棱锥V-ABC的体积为。