
 ax2+(1-a)x(a∈R且a≠0).
ax2+(1-a)x(a∈R且a≠0). ax2+(a-1)x
ax2+(a-1)x -ax+a-1=-
-ax+a-1=-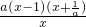 ,…(2分)
,…(2分) <1时,即a<-1时,令f′(x)>0,解得0<x<-
<1时,即a<-1时,令f′(x)>0,解得0<x<- 或x>1;
或x>1; <x<1.
<x<1. )和(1,+∞)上单调递增,在(-
)和(1,+∞)上单调递增,在(- ,1)上单调递减…(4分)
,1)上单调递减…(4分) =1时,即a=-1时,显然,函数f(x)在(0,+∞)上单调递增…(5分)
=1时,即a=-1时,显然,函数f(x)在(0,+∞)上单调递增…(5分) >1时,即-1<a<0时,令f′(x)>0,解得0<x<1或x>-
>1时,即-1<a<0时,令f′(x)>0,解得0<x<1或x>- ;
; .
. ,+∞)上单调递增,(1,-
,+∞)上单调递增,(1,- )上单调递减…(6分)
)上单调递减…(6分) )和(1,+∞)上单调递增,在(-
)和(1,+∞)上单调递增,在(- ,1)上单调递减;
,1)上单调递减; ,+∞)上单调递增,(1,-
,+∞)上单调递增,(1,- )上单调递减…(7分)
)上单调递减…(7分) a
a +(1-a)x1…①
+(1-a)x1…① a
a +(1-a)x2…②
+(1-a)x2…② a(x1+x2)+1-a](x1-x2)…③
a(x1+x2)+1-a](x1-x2)…③ =
= a(x1+x2)+1-a,
a(x1+x2)+1-a, =
= ,
, =
=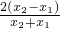 =
= ,
, =t,(t>1),上式化为:lnt=
=t,(t>1),上式化为:lnt=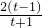 =2-
=2- ,…(11分)
,…(11分) =2…(12分)
=2…(12分) ,g′(t)=
,g′(t)= -
-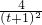 =
= ,
, =2成立.
=2成立. ax2+(a-1)x,f′(x)=-
ax2+(a-1)x,f′(x)=-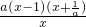 ,对a分a>0,a=0与a<0,三类讨论,对a<0再根据1与-
,对a分a>0,a=0与a<0,三类讨论,对a<0再根据1与- 的大小关系分三类讨论即可求得答案;
的大小关系分三类讨论即可求得答案; a(x1+x2)+1-a](x1-x2),假设C1在M处的切线与C2在N处的切线平线,则有
a(x1+x2)+1-a](x1-x2),假设C1在M处的切线与C2在N处的切线平线,则有 =
= a(x1+x2)+1-a,与前式联立可得:
a(x1+x2)+1-a,与前式联立可得: =
= ,设
,设 =t,(t>1),则lnt+
=t,(t>1),则lnt+ =2,构造函数g(t)=lnt+
=2,构造函数g(t)=lnt+ ,可判断g(t)在(1,+∞)上递增,g(t)>2恒成立.从而可证明C1在M处的切线与C2在N处的切线不平行.
,可判断g(t)在(1,+∞)上递增,g(t)>2恒成立.从而可证明C1在M处的切线与C2在N处的切线不平行.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省新余四中高三(下)开学数学试卷(理科)(解析版) 题型:解答题
 ax2+(1-a)x(a∈R且a≠0).
ax2+(1-a)x(a∈R且a≠0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com