
【题目】已知函数f(x)=2cosxsin(x+2φ)为偶函数,其中φ∈(0,![]() ),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
A.g(x)在区间[![]() ]上的最小值为﹣1
]上的最小值为﹣1
B.g(x)的图象可由函数f(x)的图象向上平移一个单位,再向右平移![]() 个单位长度得到
个单位长度得到
C.g(x)的图象的一个对称中心为(![]() ,0)
,0)
D.g(x)的一个单调递增区间为[0,![]() ]
]
科目:高中数学 来源: 题型:
【题目】猜商品的价格游戏, 观众甲: ![]() 主持人:高了! 观众甲:
主持人:高了! 观众甲: ![]() 主持人:低了! 观众甲:
主持人:低了! 观众甲: ![]() 主持人:高了! 观众甲:
主持人:高了! 观众甲: ![]() 主持人:低了! 观众甲:
主持人:低了! 观众甲: ![]() 主持人:低了! 则此商品价格所在的区间是 ( )
主持人:低了! 则此商品价格所在的区间是 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天数 | 25 | 50 | 100 | 25 |
若将频率视为概率,试解答如下问题:
(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;
(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近些年随着我国国民消费水平的升级,汽车产品已经逐渐进入千家万户,但是我国的城市发展水平并不能与汽车保有量增速形成平衡,城市交通问题越发突出,因此各大城市相继出现了购车限号上牌的政策.某城市采用摇号买车的限号上牌方式,申请人提供申请,经审查合格后,确认申请编码为有效编码,这时候就可以凭借申请编码参加每月一次的摇号.假设该城市有20万人参加摇号,每个月有2万个名额,每个月摇上的人退出摇号,没有摇上的人继续下个月摇号.
(1)平均每个人摇上号需要多长时间?
(2)如果每个月都有2万人补充进摇号队伍,以每个人进入摇号的月份算第一个月,他摇到号的月份设为随机变量![]() .
.
①证明:![]() 为等比数列;
为等比数列;
②假设该项政策连续实施36个月,小王是第一个月就参加摇号的人,记小王参.加摇号的次数为![]() ,试求
,试求![]() 的数学期望(精确到0.01).
的数学期望(精确到0.01).
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
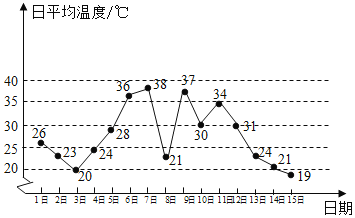
A. 这15天日平均温度的极差为![]()
B. 连续三天日平均温度的方差最大的是7日,8日,9日三天
C. 由折线图能预测16日温度要低于![]()
D. 由折线图能预测本月温度小于![]() 的天数少于温度大于
的天数少于温度大于![]() 的天数
的天数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是等比数列,
是等比数列,![]() ,
,![]() ,
,![]() .判断
.判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平面四边形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 和
和![]() 均为等边三角形,
均为等边三角形,![]()
![]() 分别是
分别是![]() 和
和![]() 的中点,将四边形
的中点,将四边形![]() 沿
沿![]() 向上翻折至四边形
向上翻折至四边形![]() 的位置,使二面角
的位置,使二面角![]() 为直二面角,如图2所示.
为直二面角,如图2所示.
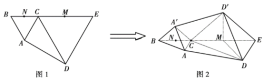
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 上点
上点![]() 作三条斜率分别为
作三条斜率分别为![]() ,
,![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,
,![]() ,与抛物线分别交于不同于
,与抛物线分别交于不同于![]() 的点
的点![]() .若
.若![]() ,
,![]() ,则以下结论正确的是( )
,则以下结论正确的是( )
A.直线![]() 过定点B.直线
过定点B.直线![]() 斜率一定
斜率一定
C.直线![]() 斜率一定D.直线
斜率一定D.直线![]() 斜率一定
斜率一定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com